Spatial Visium exploratory data analysis

Lambda Moses

2024-11-23

Introduction

This vignette provides an introduction to exploratory spatial data analysis methods via the Voyager package in the context of a Visium dataset.

library(Voyager)
library(SpatialFeatureExperiment)
library(scater)
library(scran)
library(SFEData)
library(sf)
library(ggplot2)
library(scales)
library(patchwork)
library(BiocParallel)
library(bluster)
library(dplyr)
library(reticulate)
theme_set(theme_bw(10))

<<<<<<< HEAD

=======

>>>>>>> documentation
# Specify Python version to use gget
PY_PATH <- system("which python", intern = TRUE)
use_python(PY_PATH)
py_config()

# Load gget
gget <- import("gget")

Dataset

The dataset used in this vignette is from the paper Large-scale integration of single-cell transcriptomic data captures transitional progenitor states in mouse skeletal muscle regeneration (McKellar et al. 2021). Notexin was injected into the tibialis anterior muscle of mice to induce injury, and the healing muscle was collected 2, 5, and 7 days post injury for Visium analysis. The dataset in this vignette is from the timepoint at day 2. The vignette starts with a SpatialFeatureExperiment (SFE) object.

The gene count matrix was directly downloaded from GEO. All 4992 spots, whether in tissue or not, are included. The H&E image was used for nuclei and myofiber segmentation. A subset of nuclei from randomly selected regions from all 3 timepoints were manually annotated to train a StarDist model to segment the rest of the nuclei, and the myofibers were all manually segmented. The tissue boundary was found by thresholding in OpenCV, and small polygons were removed as they are likely to be debris. Spot polygons were constructed with the spot centroid coordinates and diameter in the Space Ranger output. The in_tissue column in colData indicates which spot polygons intersect the tissue polygons, and is based on st_intersects().

Tissue boundary, nuclei, myofiber, and Visium spot polygons are stored as sf data frames in the SFE object. See the vignette of SpatialFeatureExperiment for more details on the structure of the SFE object. The SFE object of this dataset is provided in the SFEData package; we begin by downloading the data and loading it into R.

(sfe <- McKellarMuscleData("full"))
#> see ?SFEData and browseVignettes('SFEData') for documentation
#> loading from cache
#> class: SpatialFeatureExperiment 
#> dim: 15123 4992 
#> metadata(0):
#> assays(1): counts
#> rownames(15123): ENSMUSG00000025902 ENSMUSG00000096126 ...
#>   ENSMUSG00000064368 ENSMUSG00000064370
#> rowData names(6): Ensembl symbol ... vars cv2
#> colnames(4992): AAACAACGAATAGTTC AAACAAGTATCTCCCA ... TTGTTTGTATTACACG
#>   TTGTTTGTGTAAATTC
#> colData names(12): barcode col ... prop_mito in_tissue
#> reducedDimNames(0):
#> mainExpName: NULL
#> altExpNames(0):
#> spatialCoords names(2) : imageX imageY
#> imgData names(1): sample_id
#> 
#> unit: full_res_image_pixels
#> Geometries:
#> colGeometries: spotPoly (POLYGON) 
#> annotGeometries: tissueBoundary (POLYGON), myofiber_full (POLYGON), myofiber_simplified (POLYGON), nuclei (POLYGON), nuclei_centroid (POINT) 
#> 
#> Graphs:
#> Vis5A:

The H&E image of this section:

if (!file.exists("tissue_lowres_5a.jpeg")) {
    download.file("https://raw.githubusercontent.com/pachterlab/voyager/main/vignettes/tissue_lowres_5a.jpeg",
                  destfile = "tissue_lowres_5a.jpeg")
}

The image can be added to the SFE object and plotted behind the geometries, and needs to be flipped to align to the spots because the origin is at the top left for the image but bottom left for geometries.

sfe <- addImg(sfe, imageSource = "tissue_lowres_5a.jpeg", sample_id = "Vis5A", 
              image_id = "lowres", 
              scale_fct = 1024/22208)

Exploratory data analysis

Spots in tissue

While the example dataset has all Visium spots whether on tissue or not, only spots that intersect tissue are used for further analyses.

names(colData(sfe))
#>  [1] "barcode"   "col"       "row"       "x"         "y"         "dia"      
#>  [7] "tissue"    "sample_id" "nCounts"   "nGenes"    "prop_mito" "in_tissue"

Total UMI counts (nCounts), number of genes detected per spot (nGenes), and the proportion of mitochondrially encoded counts (prop_mito) have been precomputed and are in colData(sfe). The plotSpatialFeature function can be used to visualize various attributes in space: the expression of any gene, colData values, and geometry attributes in colGeometry and annotGeometry. The Visium spots are plotted as polygons reflecting their actual size relative to the tissue, rather than as points, as is the case in other packages that plot Visium data. The plotting of geometries is being performed under the hood with geom_sf.

The tissue boundary was found by thresholding the H&E image and removing small polygons that are most likely debris. The in_tissue column of colData(sfe) indicates which Visium spot polygon intersects the tissue polygon; this can be found with SpatialFeatureExperiment::annotPred().

We demonstrate the use of scran (Lun, McCarthy, and Marioni 2016) for normalization below, although we note that it is not necessarily the best approach to normalizing spatial transcriptomics data. The problem of when and how to normalize spatial transcriptomics data is non-trivial because, as the nCounts plot in space shows above, spatial autocorrelation is evident. Furthemrore, in Visium, reverse transcription occurs in situ on the spots, but PCR amplification occurs after the cDNA is dissociated from the spots. Artifacts may be subsequently introduced from the amplification step, and these would not be associated with spatial origin. Spatial artifacts may arise from the diffusion of transcripts and tissue permeablization. However, given how the total counts seem to correspond to histological regions, the total counts may have a biological component and hence should not be treated as a technical artifact to be normalized away as in scRNA-seq data normalization methods. In other words, the issue of normalization for spatial transcriptomics data, and Visium in particular, is complex and is currently unsolved.

sfe_tissue <- sfe[,colData(sfe)$in_tissue]
sfe_tissue <- sfe_tissue[rowSums(counts(sfe_tissue)) > 0,]

#clusters <- quickCluster(sfe_tissue)
#sfe_tissue <- computeSumFactors(sfe_tissue, clusters=clusters)
#sfe_tissue <- sfe_tissue[, sizeFactors(sfe_tissue) > 0]
sfe_tissue <- logNormCounts(sfe_tissue)

Myofiber and nuclei segmentation polygons are available in this dataset in the annotGeometries field. Myofibers were manually segmented, and nuclei were segmented with StarDist trained with a manually segmented subset.

annotGeometryNames(sfe_tissue)
#> [1] "tissueBoundary"      "myofiber_full"       "myofiber_simplified"
#> [4] "nuclei"              "nuclei_centroid"

From myofibers and nuclei to Visium spots

The plotSpatialFeature() function can also be used to plot attributes of geometries, i.e. the non-geometry columns in the sf data frames in the rowGeometries, colGeometries, or annotGeometries fields of the SFE object. For rowGeometries and colGeometries, such columns which are associated with the sf data frames rather than rowData or colData, are allowed because one can specify how these columns associate with the geometries (see st_agr and documentation of st_sf). When an attribute of an annotGeometry is plotted along side gene expression or colData or colGeometry attribute, the annotGeometry attribute is plotted with a different color palette to distinguish it from the column associated values.

The myofiber polygons from annotGeometries can be plotted as shown below, colored by cross section area as observed in the tissue section. The aes_use argument is set to color rather than fill (default for polygons) to only plot the Visium spot outlines to make the myofiber polygons more visible. The fill argument is set to NA to make the Visium spots look hollow, and the size argument controls the thickness of the outlines. The annot_aes argument specifies which column in the annotGeometry to use to specify the values of an aesthstic, just like aes in ggplot2 (aes_string to be precise, since tidyeval is not used here). The annot_fixed argument (not used here) can set the fixed size, alpha, color, and etc. for the annotGeometry.

plotSpatialFeature(sfe_tissue, features = "nCounts", 
                   colGeometryName = "spotPoly",
                   annotGeometryName = "myofiber_simplified", 
                   aes_use = "color", linewidth = 0.5, fill = NA,
                   annot_aes = list(fill = "area"))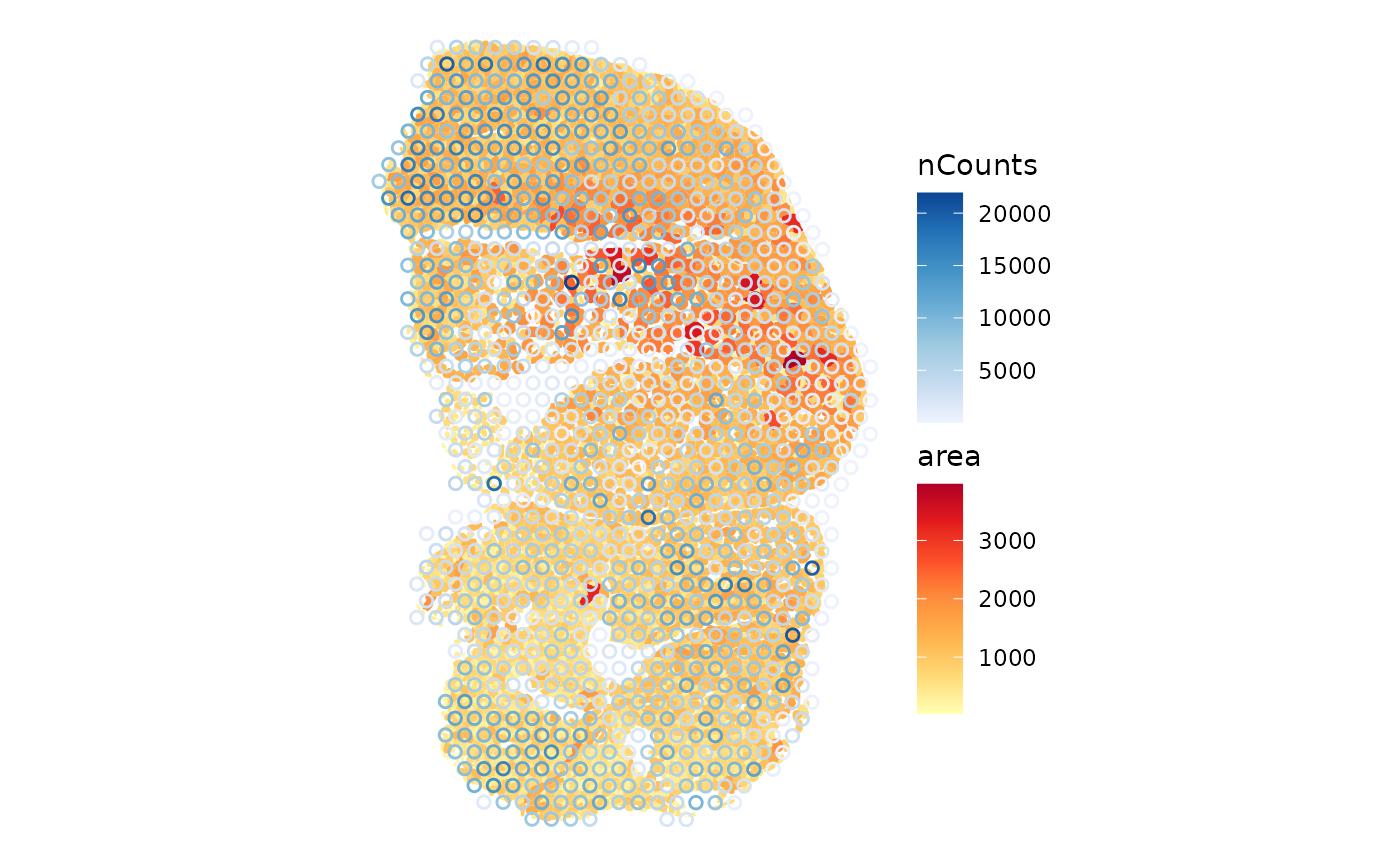

The larger myofibers seem to have fewer total counts, possibly because the larger size of these myofibers dilutes the transcripts. This hints at the need for a normalization procedure.

With SpatialFeatureExperiment, we can find the number of myofibers and nuclei that intersect each Visium spot. The predicate can be anything implemented in sf, so for example, the number of nuclei fully covered by each Visium spot can also be found. The default predicate is st_intersects().

colData(sfe_tissue)$n_myofibers <- 
  annotNPred(sfe_tissue, colGeometryName = "spotPoly",
             annotGeometryName = "myofiber_simplified")

plotSpatialFeature(sfe_tissue, features = "n_myofibers", 
                   colGeometryName = "spotPoly", image = "lowres", color = "black",
                   linewidth = 0.1)

There is no one-to-one mapping between Visium spots and myofibers. However, we can relate attributes of myofibers to gene expression detected at the Visium spots. One way to do so is to summarize the attributes of all myofibers that intersect (or choose another better predicate implemented in sf) each spot, such as to calculate the mean, median, or sum. This can be done with the annotSummary() function in SpatialFeatureExperiment. The default predicate is st_intersects(), and the default summary function is mean().

colData(sfe_tissue)$mean_myofiber_area <- 
  annotSummary(sfe_tissue, "spotPoly", "myofiber_simplified", 
               annotColNames = "area")[,1] # it always returns a data frame

# The gray spots don't intersect any myofiber
plotSpatialFeature(sfe_tissue, "mean_myofiber_area", "spotPoly", image = "lowres", 
                   color = "black", linewidth = 0.1)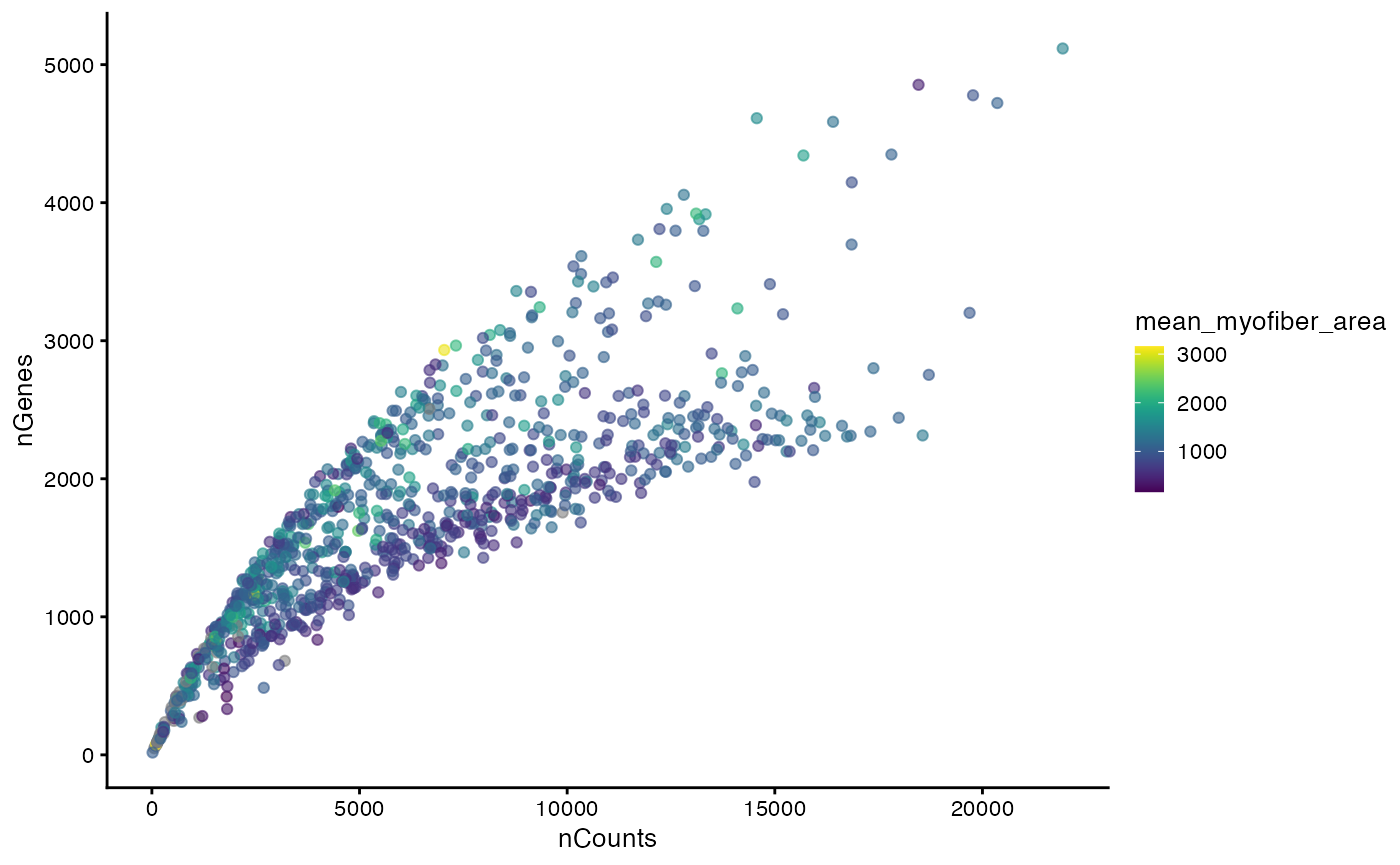

This reveals the relationship between the mean area of myofibers intersecting each Visium spot and other aspects of the spots, such as total counts and gene expression.

The NAs designate spots not intersecting any myofibers, e.g. those in the inflammatory region.

In the Basic Visium vignette, we encountered two mysterious branches and two clusters in the nGenes vs. nCounts plot and the proportion of mitochondrial counts vs. nCounts plot. Now we see that the two clusters seem to be related to myofiber size.

plotColData(sfe_tissue, x = "nCounts", y = "nGenes", colour_by = "mean_myofiber_area")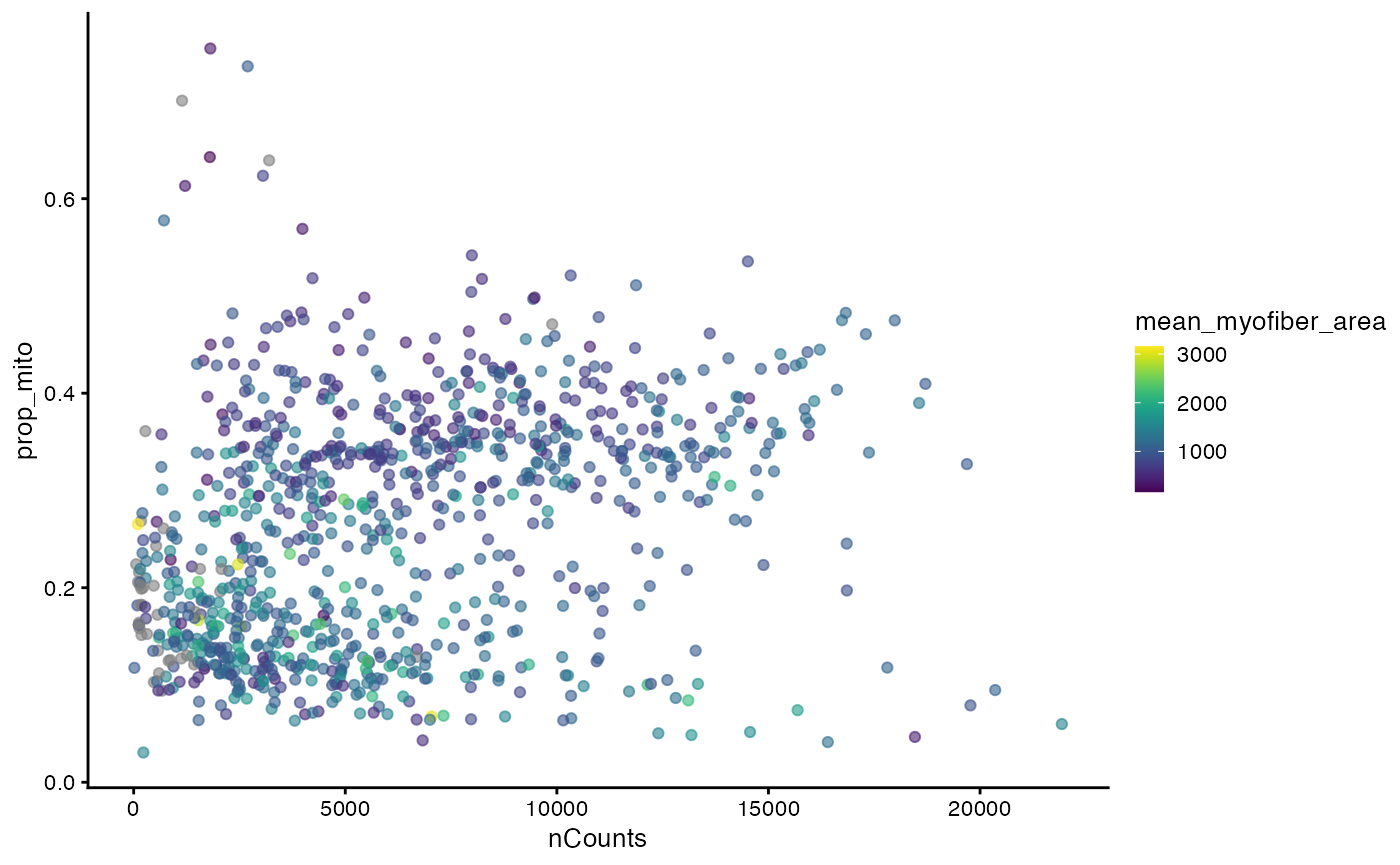

plotColData(sfe_tissue, x = "nCounts", y = "prop_mito", colour_by = "mean_myofiber_area")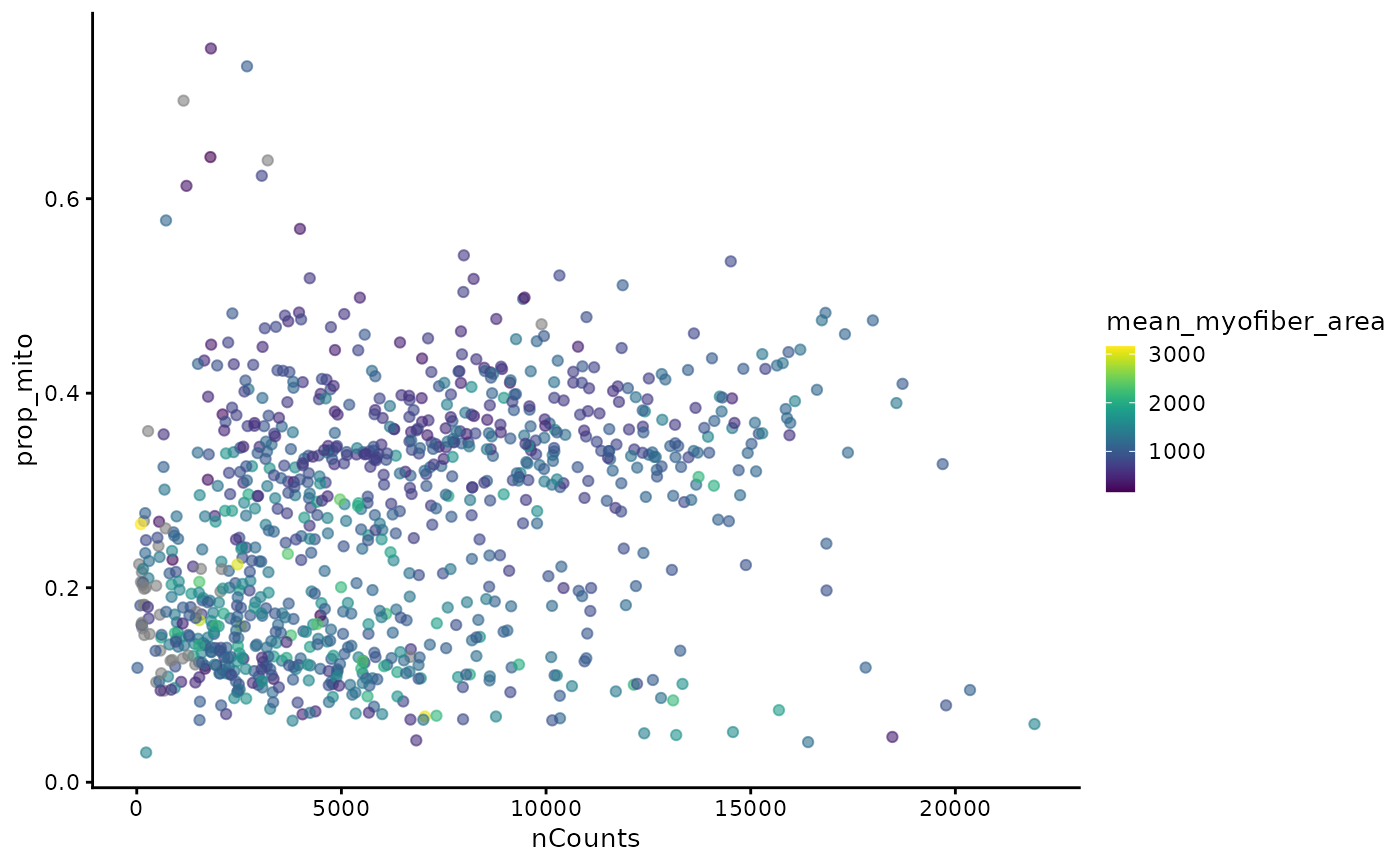

Myofiber types

Marker genes: Myh7 (Type I, slow twitch, aerobic), Myh2 (Type IIa, fast twitch, somewhat aerobic), Myh4 (Type IIb, fast twitch, anareobic), Myh1 (Type IIx, fast twitch, anaerobic), from this protocol (Wang, Yue, and Kuang 2017)

markers <- c(I = "Myh7", IIa = "Myh2", IIb = "Myh4", IIx = "Myh1")

We can use the gget search and gget info modules from the gget package to get the Ensembl IDs and additional information (for example their NCBI description) for these marker genes: <<<<<<< HEAD

=======

>>>>>>> documentation
gget_search <- gget$search(list("Myh7", "Myh2", "Myh4", "Myh1"), species="mouse")
gget_search <- gget_search[gget_search$gene_name %in% list("Myh7", "Myh2", "Myh4", "Myh1"), ]
gget_search

<<<<<<< HEAD

=======

>>>>>>> documentation
gget_info <- gget$info(gget_search$ensembl_id)

rownames(gget_info) <- gget_info$primary_gene_name
select(gget_info, ncbi_description)

We first examine the Type I myofibers. This is a fast twitch muscle, so we don’t expect many slow twitch Type I myofibers. Row names in sfe_tissue are Ensembl IDs in order to avoid ambiguity as sometimes multiple Ensembl IDs have the same gene symbol and some genes have aliases. However, gene symbols are shorter and more human readable than Ensembl IDs, and are better suited to display on plots. In the plotSpatialFeature() function and other functions in Voyager, even when the row names are recorded as Ensembl IDs, the features argument can take gene symbols with the swap_rownames argument indicating a column in rowData(sfe) that stores the gene symbols. Gene symbols is then also shown in plots instead of Ensembl IDs. If one gene symbol matches multiple Ensembl IDs in the dataset, then a warning will be given.

The exprs_values argument specifies the assay to use, which is by default “logcounts”, i.e. the log normalized data. This default may or may not be suitable in practice given that total UMI counts may have biological relevance in spatial data. Therefore, we plot both the raw counts and the log normalized counts:

# Function specific for this vignette, with some hard coded values
plot_counts_logcounts <- function(sfe, feature) {
  p1 <- plotSpatialFeature(sfe, feature, "spotPoly",
                   annotGeometryName = "myofiber_simplified", 
                   annot_aes = list(fill = "area"), swap_rownames = "symbol", 
                   exprs_values = "counts", aes_use = "color", linewidth = 0.5,
                   fill = NA) +
    ggtitle("Raw counts")
  p2 <- plotSpatialFeature(sfe, feature, "spotPoly",
                   annotGeometryName = "myofiber_simplified", 
                   annot_aes = list(fill = "area"), swap_rownames = "symbol", 
                   exprs_values = "logcounts", aes_use = "color", linewidth = 0.5,
                   fill = NA) +
    ggtitle("Log normalized counts")
  p1 + p2 +
    plot_annotation(title = feature)
}

plot_counts_logcounts(sfe_tissue, markers["I"])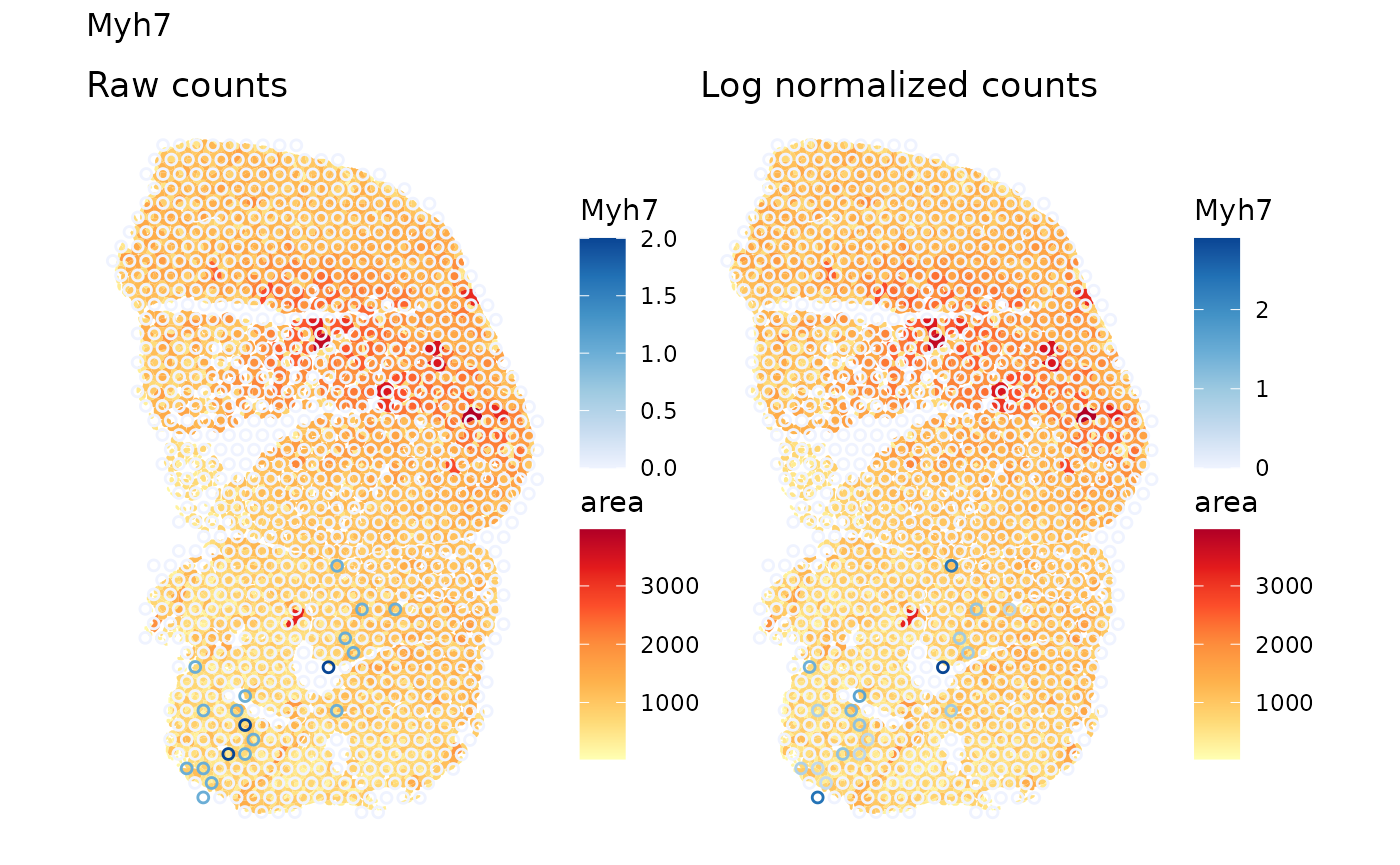

A marker gene for type IIa myofibers is shown above. It is straightforward to modify the plotting to display markers for type IIb and type IIx myofibers:

plot_counts_logcounts(sfe_tissue, markers["IIa"])

Type IIa myofibers also tend to be clustered together on left side of the tissue.

As SFE inherits from SCE, the non-spatial EDA plots from the scater package can also be used:

plotColData(sfe_tissue, x = "mean_myofiber_area", y = "prop_mito", 
            colour_by = markers["IIa"], by_exprs_values = "logcounts", 
            swap_rownames = "symbol")
#> Warning: Removed 36 rows containing missing values or values outside the scale range
#> (`geom_point()`).

Plotting proportion of mitochondrial counts vs. mean myofiber area, we see two clusters, one with higher proportion of mitochondrial counts and smaller area, and another with lower proportion of mitochondrial counts and on average slightly larger area. Type IIa myofibers tend to have smaller area and a larger proportion of mitochondrial counts.

Spatial neighborhood graphs

A spatial neighborhood graph is required to compute spatial dependency metrics such as Moran’s I and Geary’s C. The SpatialFeatureExperiment package wraps methods in spdep to find spatial neighborhood graphs, which are stored within the SFE object (see spdep documentation for gabrielneigh(), knearneigh(), poly2nb(), and tri2nb()). The Voyager package then uses these graphs for spatial dependency analyses, again based on spdep in this first version, but methods from other geospatial packages, some of which also use the spatial neighborhood graphs, may be added later.

For Visium, where the spots are in a hexagonal grid, the spatial neighborhood graph is straightforward. However, for spatial technologies with single cell resolution, e.g. MERFISH, different methods can be used to find the spatial neighborhood graph. In this example, the method “poly2nb” was used for myofibers, and it identifies myofiber polygons that physically touch each other. zero.policy = TRUE will allow for singletons, i.e. nodes without neighbors in the graph; in the inflamed region, there are more singletons. We have not yet benchmarked spatial neighborhood construction methods to determine which is the “best” for different technologies; the particular method used here is for demonstration purposes and may not be the best in practice:

colGraph(sfe_tissue, "visium") <- findVisiumGraph(sfe_tissue)
annotGraph(sfe_tissue, "myofiber_poly2nb") <- 
  findSpatialNeighbors(sfe_tissue, type = "myofiber_simplified", MARGIN = 3,
                       method = "poly2nb", zero.policy = TRUE)
#> Warning in (function (pl, row.names = NULL, snap = NULL, queen = TRUE, useC = TRUE, : some observations have no neighbours;
#> if this seems unexpected, try increasing the snap argument.
#> Warning in (function (pl, row.names = NULL, snap = NULL, queen = TRUE, useC = TRUE, : neighbour object has 75 sub-graphs;
#> if this sub-graph count seems unexpected, try increasing the snap argument.

The plotColGraph() function plots the graph in space associated with a colGeometry, along with the geometry of interest.

plotColGraph(sfe_tissue, colGraphName = "visium", colGeometryName = "spotPoly") +
    theme_void()

Similarly, the plotAnnotGraph() function plots the graph associated with an annotGeometry, along with the geometry of interest.

plotAnnotGraph(sfe_tissue, annotGraphName = "myofiber_poly2nb", 
               annotGeometryName = "myofiber_simplified") + theme_void()

There is no plotRowGraph yet since we haven’t worked with a dataset where spatial graphs related to genes are relevant, although the SFE object supports row graphs.

Exploratory spatial data analysis

All spatial autocorrelation metrics in this package can be computed directly on a vector or a matrix rather than an SFE object. The user interface emulates those of dimension reductions in the scater package (e.g. calculateUMAP() that takes in a matrix or SCE object and returns a matrix, and runUMAP() that takes in an SCE object and adds the results to the reducedDims field of the SCE object). So calculate* functions take in a matrix or an SFE object and directly return the results (format of the results depends on the structure of the results), while run* functions take in an SFE object and add the results to the object. In addition, colData* functions compute the metrics for numeric variables in colData. colGeometry* functions compute the metrics for numeric columns in a colGeometry. annotGeometry* functions compute the metrics for numeric columns in a annotGeometry.

Univariate global

Voyager supports many univariate global spatial autocorrelation implemented in spdep for ESDA: Moran’s I and Geary’s C, permutation testing for Moran’s I and Geary’s C, Moran plot, and correlograms. In addition, beyond spdep, Voyager can cluster Moran plots and correlograms. Plotting functions taking in SFE objects are implemented to plot the results with ggplot2 and with more customization options than spdep plotting functions. The functions calculateUnivariate(), runUnivariate(), colDataUnivariate(), colGeometryUnivariate(), and annotGeometryUnivariate() compute univariate spatial statistics. The argument type, which indicates the corresponding function names in spdep, determines which spatial statistics are computed.

All univariate global methods in Voyager are listed here:

listSFEMethods(variate = "uni", scope = "global")
#>              name                                           description
#> 1           moran                                             Moran's I
#> 2           geary                                             Geary's C
#> 3        moran.mc                    Moran's I with permutation testing
#> 4        geary.mc                    Geary's C with permutation testing
#> 5    sp.mantel.mc Mantel-Hubert spatial general cross product statistic
#> 6      moran.test                                        Moran's I test
#> 7      geary.test                                        Geary's C test
#> 8    globalG.test                                         Global G test
#> 9  sp.correlogram                                           Correlogram
#> 10      variogram                                  Variogram with model
#> 11  variogram_map                                         Variogram map

When calling calculate*variate() or run*variate(), the type (2nd) argument takes either an SFEMethod object (see SFEMethod() and vignette on SFEMethod) or a string that matches an entry in the name column in the data frame returned by listSFEMethods().

To demonstrate spatial autocorrelation in gene expression, top highly variable genes (HVGs) are used. The HVGs are found with the scran method.

dec <- modelGeneVar(sfe_tissue)
hvgs <- getTopHVGs(dec, n = 50)

A global statistic yields one result for the entire dataset.

Moran’s I

There are several ways to quantify spatial autocorrelation, the most common of which is Moran’s I:

$$I = \frac{n}{\sum_{i=1}^n \sum_{j=1}^n w_{ij}} \frac{\sum_{i=1}^n \sum_{j=1}^n w_{ij} (x_i - \bar{x})(x_j - \bar{x})}{\sum_{i=1}^n (x_i - \bar{x})^2},$$

where $n$ is the number of spots or locations, $i$ and $j$ are different locations, or spots in the Visium context, $x$ is a variable with values at each location, and $w_{ij}$ is a spatial weight, which can be inversely proportional to distance between spots or an indicator of whether two spots are neighbors, subject to various definitions of neighborhood and whether to normalize the number of neighbors. The spdep package uses the neighborhood.

Moran’s I can be understood as the Pearson correlation between the value at each location and the average value at its neighbors. Just like Pearson correlation, Moran’s I is generally bound between -1 and 1, where positive value indicates positive spatial autocorrelation and negative value indicates negative spatial autocorrelation.

Upon visual inspection, total UMI counts per spot seem to have spatial autocorrelation. A spatial neighborhood graph is required to compute Moran’s I, and is specified with the listw argument.

For matrices, the rows are the features, as in the gene count matrix.

# Directly use vector or matrix, and multiple features can be specified at once
calculateUnivariate(t(colData(sfe_tissue)[,c("nCounts", "nGenes")]), 
                    type = "moran",
                    listw = colGraph(sfe_tissue, "visium"))
#> DataFrame with 2 rows and 2 columns
#>             moran         K
#>         <numeric> <numeric>
#> nCounts  0.528705   3.00082
#> nGenes   0.384028   3.88036

“moran” is Moran’s I, and K is sample kurtosis.

To add the results to the SFE object, specifically for colData:

sfe_tissue <- colDataUnivariate(sfe_tissue, features = c("nCounts", "nGenes"),
                                colGraphName = "visium", type = "moran")
colFeatureData(sfe_tissue)[c("nCounts", "nGenes"),]
#> DataFrame with 2 rows and 2 columns
#>         moran_Vis5A   K_Vis5A
#>           <numeric> <numeric>
#> nCounts    0.528705   3.00082
#> nGenes     0.384028   3.88036

For colData, the results are added to colFeatureData(sfe), and features for which Moran’s I is not calculated have NA. The column names of featureData distinguishes between different samples (there’s only one sample in this dataset), and are parsed by plotting functions.

To add the results to the SFE object, specifically for geometries: Here “area” is the area of the cross section of each myofiber as seen in this tissue section and “eccentricity” is the eccentricity of the ellipse fitted to each myofiber.

# Remember zero.policy = TRUE since there're singletons
sfe_tissue <- annotGeometryUnivariate(sfe_tissue, type = "moran",
                                      features = c("area", "eccentricity"), 
                                      annotGeometryName = "myofiber_simplified",
                                      annotGraphName = "myofiber_poly2nb", 
                                      zero.policy = TRUE)
head(attr(annotGeometry(sfe_tissue, "myofiber_simplified"), "featureData"))
#> DataFrame with 6 rows and 2 columns
#>              moran_Vis5A   K_Vis5A
#>                <numeric> <numeric>
#> lyr.1                 NA        NA
#> area            0.327888   4.95675
#> perimeter             NA        NA
#> eccentricity    0.110938   3.26913
#> theta                 NA        NA
#> sine_theta            NA        NA

For a non-geometry column in a colGeometry, colGeometryUnivariate() is like annotGeometryUnivariate() here, but none of the colGeometries in this dataset has extra columns.

For gene expression, the logcounts assay is used by default (use the exprs_values argument to change the assay), though this may or may not be best practice. If the metrics are computed for a large number of features, parallel computing is supported, with BiocParallel, with the BPPARAM argument.

sfe_tissue <- runUnivariate(sfe_tissue, type = "moran", features = hvgs, 
                            colGraphName = "visium", 
                            BPPARAM = MulticoreParam(2))
rowData(sfe_tissue)[head(hvgs),]
#> DataFrame with 6 rows and 8 columns
#>                               Ensembl      symbol            type     means
#>                           <character> <character>     <character> <numeric>
#> ENSMUSG00000029304 ENSMUSG00000029304        Spp1 Gene Expression   1.63722
#> ENSMUSG00000050708 ENSMUSG00000050708        Ftl1 Gene Expression   2.37981
#> ENSMUSG00000050335 ENSMUSG00000050335      Lgals3 Gene Expression   1.43189
#> ENSMUSG00000021939 ENSMUSG00000021939        Ctsb Gene Expression   2.73117
#> ENSMUSG00000021190 ENSMUSG00000021190        Lgmn Gene Expression   1.11278
#> ENSMUSG00000018893 ENSMUSG00000018893          Mb Gene Expression   2.11118
#>                         vars       cv2 moran_Vis5A   K_Vis5A
#>                    <numeric> <numeric>   <numeric> <numeric>
#> ENSMUSG00000029304   60.1583   22.4430    0.734937   1.63516
#> ENSMUSG00000050708  162.1931   28.6384    0.665563   1.81841
#> ENSMUSG00000050335   48.0739   23.4471    0.741474   1.68098
#> ENSMUSG00000021939  131.6232   17.6455    0.708362   1.86896
#> ENSMUSG00000021190   21.4505   17.3228    0.659916   1.66838
#> ENSMUSG00000018893   74.1782   16.6428    0.675840   1.82510

Geary’s C

Another spatial autocorrelation metric is Geary’s C, defined as:

$$C = \frac{(n-1)}{2\sum_{i=1}^n \sum_{j=1}^n w_{ij}} \frac{\sum_{i=1}^n \sum_{j=1}^n w_{ij}(x_i - x_j)^2}{{\sum_{i=1}^n (x_i - \bar{x})^2}}$$

Geary’s C below 1 indicates positive spatial autocorrelation, and above 1 indicates negative spatial autocorrelation.

To compute Geary’s C for features of interest replace type = "moran" in the previous section with type = "geary", and add the results to the SFE object. For example, for colData

sfe_tissue <- colDataUnivariate(sfe_tissue, features = c("nCounts", "nGenes"),
                                colGraphName = "visium", type = "geary")
colFeatureData(sfe_tissue)[c("nCounts", "nGenes"),]
#> DataFrame with 2 rows and 3 columns
#>         moran_Vis5A   K_Vis5A geary_Vis5A
#>           <numeric> <numeric>   <numeric>
#> nCounts    0.528705   3.00082    0.474892
#> nGenes     0.384028   3.88036    0.605797

There’s only one column for K since it’s the same for Moran’s I and Geary’s C. Here both Moran’s I and Geary’s C suggest positive spatial autocorrelation for nCounts and nGenes.

Other univariate global methods, including permutation testing for Moran’s I and Geary’s C, correlograms, and Moran scatter plot can also be called with functions such as runUnivariate, by specifying the type argument. See documentation of runUnivariate to see the available methods and see documentation of the corresponding spdep functions to see the extra arguments required for each method.

Permutation testing

To establish whether the spatial autocorrelation is statistically significant, the moran.test() function in spdep can be used. It provides a p-value, but the p-value may not be accurate if the data is not normally distributed. As gene expression data is generally not normally distributed and data normalization doesn’t always work well, we use permutation testing to test the significance of Moran’s I and Geary’s C, wrapping moran.mc() in spdep. The “mc” stands for Monte Carlo. The nsim argument specifies the number of simulations.

The following adds the results to the SFE object:

set.seed(29)
sfe_tissue <- colDataUnivariate(sfe_tissue, features = c("nCounts", "nGenes"), 
                                colGraphName = "visium", nsim = 1000,
                                type = "moran.mc")
colFeatureData(sfe_tissue)[c("nCounts", "nGenes"),]
#> DataFrame with 2 rows and 9 columns
#>         moran_Vis5A   K_Vis5A geary_Vis5A moran.mc_statistic_Vis5A
#>           <numeric> <numeric>   <numeric>                <numeric>
#> nCounts    0.528705   3.00082    0.474892                 0.528705
#> nGenes     0.384028   3.88036    0.605797                 0.384028
#>         moran.mc_parameter_Vis5A moran.mc_p.value_Vis5A
#>                        <numeric>              <numeric>
#> nCounts                     1001            0.000999001
#> nGenes                      1001            0.000999001
#>         moran.mc_alternative_Vis5A  moran.mc_method_Vis5A
#>                        <character>            <character>
#> nCounts                    greater Monte-Carlo simulati..
#> nGenes                     greater Monte-Carlo simulati..
#>                                 moran.mc_res_Vis5A
#>                                             <list>
#> nCounts    -0.01090202, 0.00921862,-0.00293951,...
#> nGenes  -0.000585631, 0.035577943,-0.002816707,...

Note that while the test is performed for multiple features, the p-values here are not corrected for multiple hypothesis testing.

The results can be plotted:

plotMoranMC(sfe_tissue, c("nCounts", "nGenes"))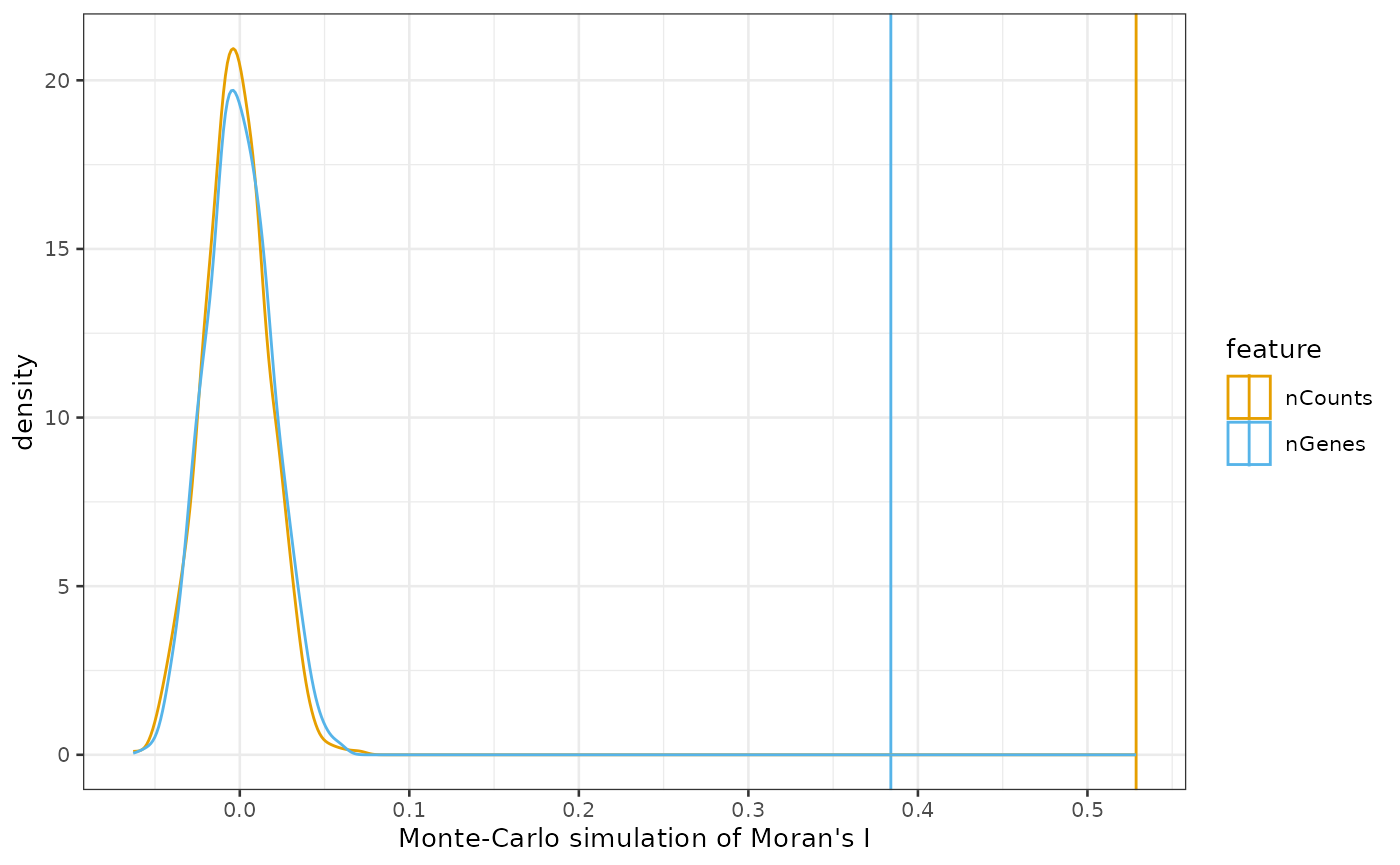

By default, the colorblind friendly palette from dittoSeq is used for categorical variables. The density plot is of Moran’s I from the simulations where the values are permuted and disconnected from spatial locations, and the vertical line is the actual Moran’s I value. The simulation indicates that the actual Moran’s I is much higher than that from the simulations where the values are dissociated from spatial locations and permuted among the locations, indicating that spatial autocorrelation is very significant.

Use type = "geary.mc" for permutation testing for Geary’s C.

The spdep package can also compute p-values of Moran’s I analytically, but the theory behind the mean and variance of the null distribution of Moran’s I assumes normal distribution of the data, while gene expression data is generally non-normal. However, according to (Griffith 2010), with large sample size (“preferably at least 100”), mean and variance of Moran’s I of several iid non-normal simulated datasets (including negative binomial, which is commonly used to model gene expression data) don’t seem to deviate much from the values expected from normally distributed data. Spatial transcriptomics datasets typically have thousands or more spots or cells, so sample size is most likely large enough. Hence using the analytical test on non-normal data might not be too bad. However, with large sample size, a minuscule difference can create very significant p-values. Here we perform the analytical test for Moran’s I:

sfe_tissue <- colDataUnivariate(sfe_tissue, features = c("nCounts", "nGenes"), 
                                colGraphName = "visium", type = "moran.test")
names(colFeatureData(sfe_tissue))
#>  [1] "moran_Vis5A"                        "K_Vis5A"                           
#>  [3] "geary_Vis5A"                        "moran.mc_statistic_Vis5A"          
#>  [5] "moran.mc_parameter_Vis5A"           "moran.mc_p.value_Vis5A"            
#>  [7] "moran.mc_alternative_Vis5A"         "moran.mc_method_Vis5A"             
#>  [9] "moran.mc_res_Vis5A"                 "moran.test_statistic_Vis5A"        
#> [11] "moran.test_p.value_Vis5A"           "moran.test_alternative_Vis5A"      
#> [13] "moran.test_method_Vis5A"            "moran.test_Moran.I.statistic_Vis5A"
#> [15] "moran.test_Expectation_Vis5A"       "moran.test_Variance_Vis5A"

Now compare the p-values from permutation and analytical test; in both cases here, the default alternative hypothesis is positive spatial autocorrelation:

# permutation
colFeatureData(sfe_tissue)[c("nCounts", "nGenes"), c("moran.mc_p.value_Vis5A", "moran.test_p.value_Vis5A")]
#> DataFrame with 2 rows and 2 columns
#>         moran.mc_p.value_Vis5A moran.test_p.value_Vis5A
#>                      <numeric>                <numeric>
#> nCounts            0.000999001             5.41958e-163
#> nGenes             0.000999001              2.82666e-87

The p-values from permutation are limited by the number of permutations (1000 here). Either way, both permutation and analytical tests indicate very significant positive spatial autocorrelation.

A limitation of permutation testing of Moran’s I is that it assumes that each permutation of the values among the locations is equally likely, which is not necessarily true. For instance, in epidemiology, disease rate in regions with small population more likely assumes more extreme values (Assunção and Reis 1999), which is analogous to rare cell types and lowly expressed genes in histological space given that we divide by total UMI counts per spot. The extent this happens may depend on tissue, gene of interest, technology, and data normalization method.

Correlogram

In a correlogram, spatial autocorrelation of higher orders of neighbors (e.g. second order neighbors are neighbors of neighbors) is calculated to see how it decays over the orders. In Visium, with the regular hexagonal grid, order of neighbors is a proxy for distance. For more irregular patterns such as single cells, different methods to find the spatial neighbors may give different results.

For colData, Moran’s I correlogram is computed with

sfe_tissue <- runUnivariate(sfe_tissue, hvgs[1:2], colGraphName = "visium", 
                            order = 10, type = "sp.correlogram")

The results can be plotted with plotCorrelogram:

plotCorrelogram(sfe_tissue, hvgs[1:2], swap_rownames = "symbol")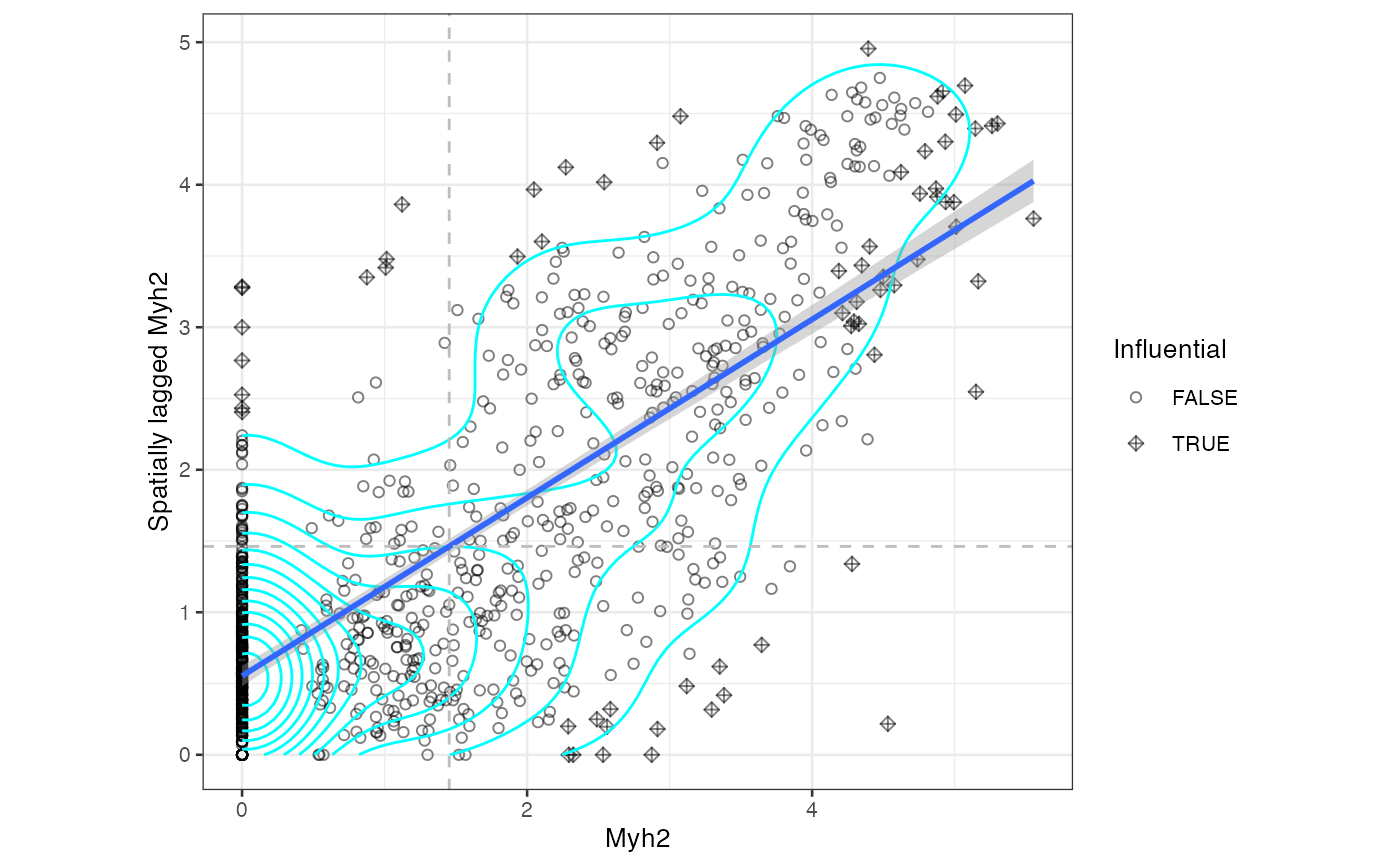

The error bars are twice the standard deviation of the Moran’s I value. The standard deviation and p-values (null hypothesis is that Moran’s I is 0) come from moran.test() (for Geary’s C correlogram, geary.test()); these should be taken with a grain of salt for data that is not normally distributed. The p-values have been corrected for multiple hypothesis testing across all orders and features. As usual, . means p < 0.1, * means p < 0.05, ** means p < 0.01, and *** means p < 0.001.

Again, this can be done for Geary’s C, colData, annotGeometry, and etc.

Univariate local

Local statistics yield a result at each location rather than the whole dataset, while global statistics may obscure local heterogeneity. See (Fotheringham 2009) for an interesting discussion of relationships between global and local spatial statistics. Local statistics are stored in the localResults field of the SFE object, which can be accessed by the localResult() or localResults() functions in the SpatialFeatureExperiment package.

All univariate local methods in Voyager are listed here:

listSFEMethods(variate = "uni", scope = "local")
#>               name                                          description
#> 1       localmoran                                      Local Moran's I
#> 2  localmoran_perm                  Local Moran's I permutation testing
#> 3           localC                                      Local Geary's C
#> 4      localC_perm                  Local Geary's C permutation testing
#> 5           localG                                      Getis-Ord Gi(*)
#> 6      localG_perm             Getis-Ord Gi(*) with permutation testing
#> 7             LOSH                     Local spatial heteroscedasticity
#> 8          LOSH.mc Local spatial heteroscedasticity permutation testing
#> 9          LOSH.cs     Local spatial heteroscedasticity Chi-square test
#> 10      moran.plot                                   Moran scatter plot

Moran scatter plot

In the Moran scatter plot (Anselin1996-mo?), the x axis is the value at a spot, and the y axis is the average value of the neighbors. The slope of the fitted line is Moran’s I. Sometimes clusters appear in this plot, showing different kinds of neighborhoods.

For gene expression, to use one gene (log normalized value) to demonstrate:

sfe_tissue <- runUnivariate(sfe_tissue, "Myh2", colGraphName = "visium", 
                            type = "moran.plot", swap_rownames = "symbol")

moranPlot(sfe_tissue, "Myh2", graphName = "visium", swap_rownames = "symbol")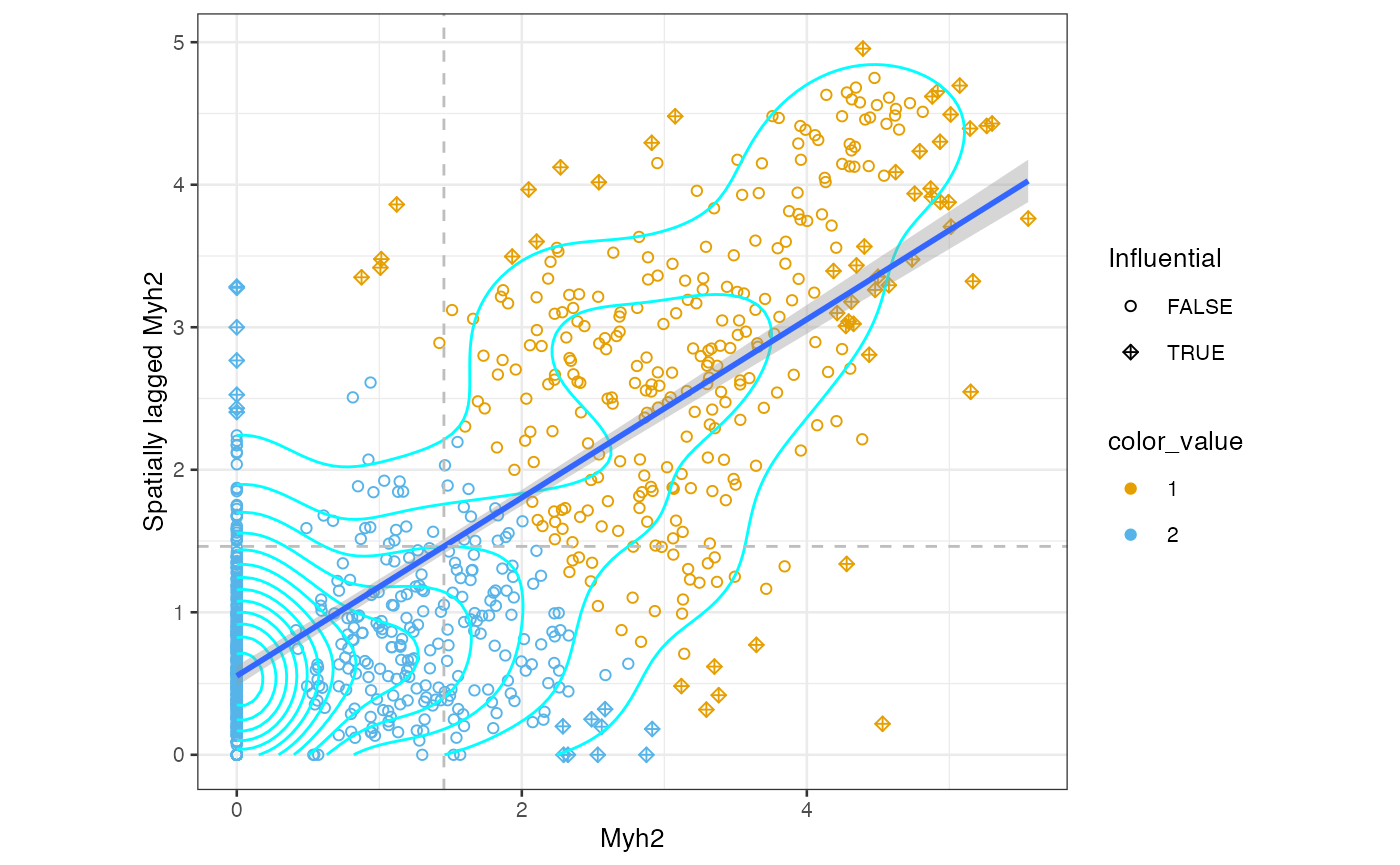

The dashed lines mark the mean in Myh2 and spatially lagged Myh2. There are no singletons here. Some Visium spots with lower Myh2 expression have neighbors that don’t express Myh2 but spots that don’t express Myh2 usually have at least some neighbors that do. There are twp main clusters for spots whose neighbors do express Myh2: those with high (above average) expression whose neighbors also have high expression, and those with low expression whose neighbors also have low expression. Other features may show different kinds of clusters. We can use k-means clustering to identify clusters, though any clustering method supported by the bluster package can be used.

set.seed(29)
clusts <- clusterMoranPlot(sfe_tissue, "Myh2", BLUSPARAM = KmeansParam(2),
                           swap_rownames = "symbol")

We can use the gget search module to get the Ensembl ID for Myh2: <<<<<<< HEAD

=======

>>>>>>> documentation
gget$search("Myh2", species="mouse")

moranPlot(sfe_tissue, "Myh2", graphName = "visium", 
          color_by = clusts$ENSMUSG00000033196, swap_rownames = "symbol")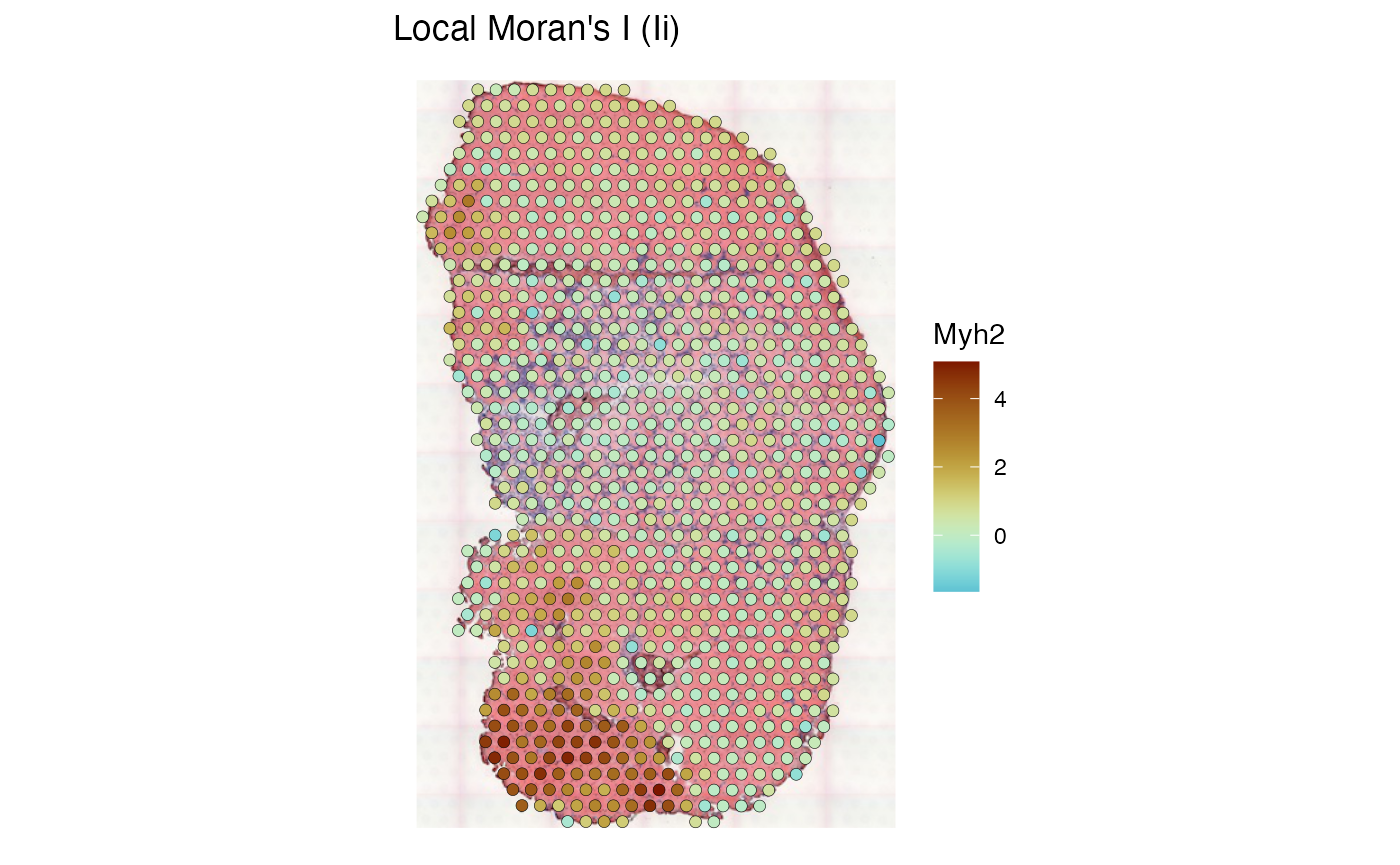

Plot the clusters in space

colData(sfe_tissue)$Myh2_moranPlot_clust <- clusts$ENSMUSG00000033196
plotSpatialFeature(sfe_tissue, "Myh2_moranPlot_clust", colGeometryName = "spotPoly",
                   image = "lowres", color = "black", linewidth = 0.1)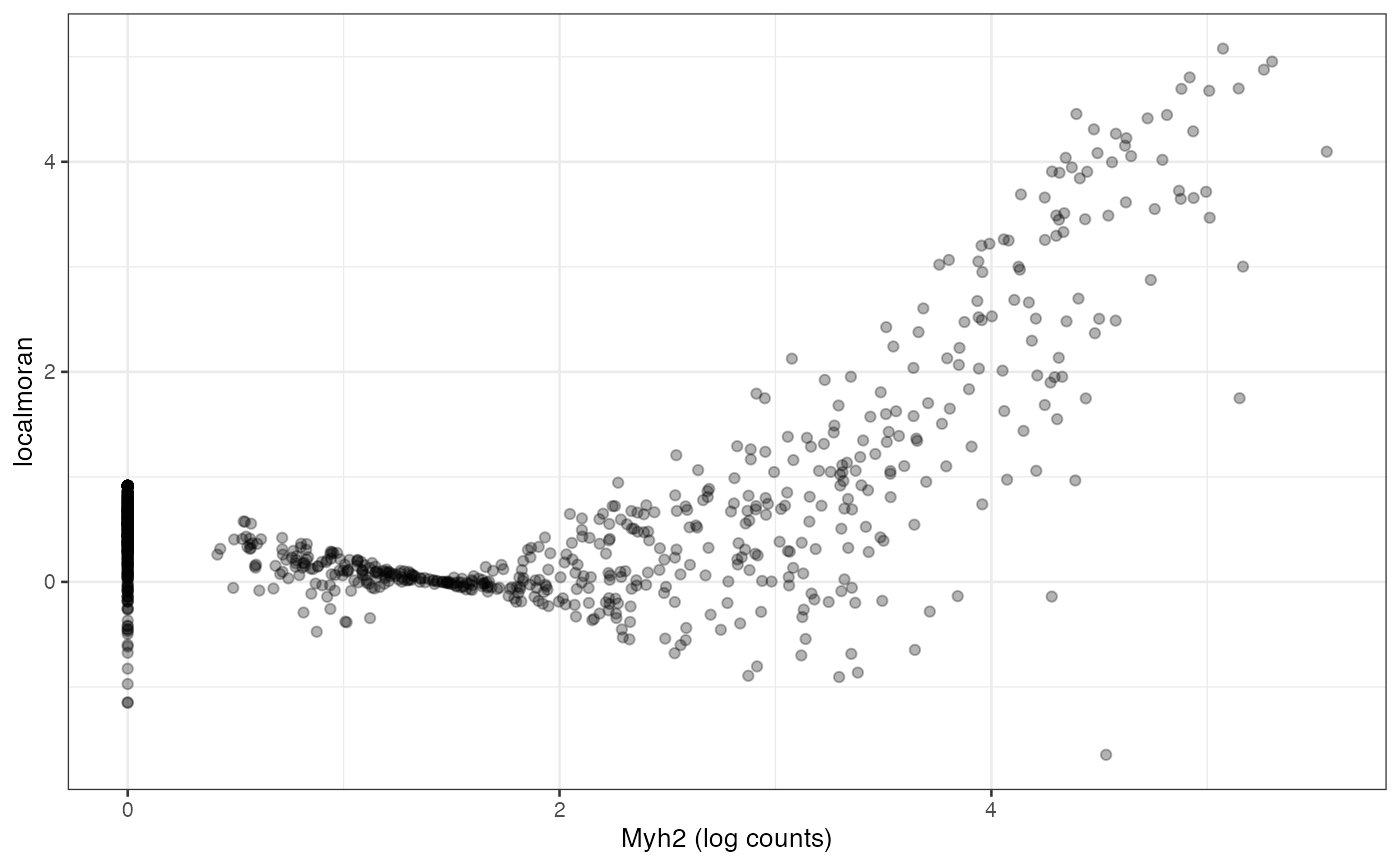

This can also be done for colData, annotGeometry, and etc. as in Moran’s I and permutation testing.

Local Moran’s I

To recap, global Moran’s I is defined as

$$I = \frac{n}{\sum_{i=1}^n \sum_{j=1}^n w_{ij}} \frac{\sum_{i=1}^n \sum_{j=1}^n w_{ij} (x_i - \bar{x})(x_j - \bar{x})}{\sum_{i=1}^n (x_i - \bar{x})^2}.$$

Local Moran’s I (Anselin 1995) is defined as

$$I_i = (n-1)\frac{(x_i - \bar{x})\sum_{j=1}^n w_{ij} (x_j - \bar{x})}{\sum_{i=1}^n (x_i - \bar{x})^2}.$$

It’s similar to global Moran’s I, but the values at locations $i$ are not summed and there’s no normalization by the sum of spatial weights.

sfe_tissue <- runUnivariate(sfe_tissue, type = "localmoran", features = "Myh2",
                            colGraphName = "visium", swap_rownames = "symbol")

It is useful to plot the log normalized Myh2 gene expression as context to interpret the local results:

plotSpatialFeature(sfe_tissue, features = "Myh2", colGeometryName = "spotPoly",
                   swap_rownames = "symbol", image_id = "lowres", color = "black",
                   linewidth = 0.1)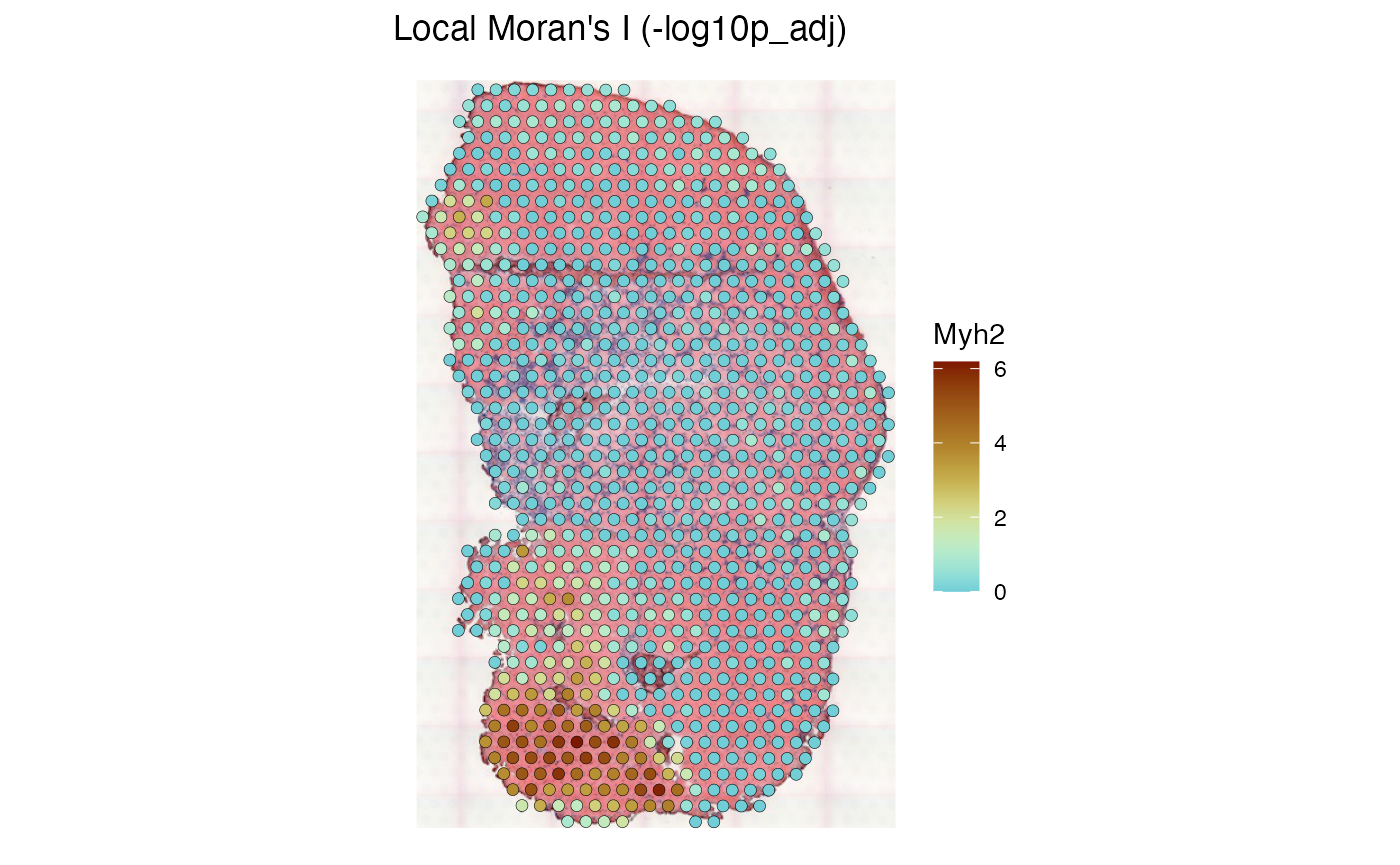

plotLocalResult(sfe_tissue, "localmoran", features = "Myh2", 
                colGeometryName = "spotPoly",divergent = TRUE,
                diverge_center = 0, image_id = "lowres", 
                swap_rownames = "symbol", color = "black",
                linewidth = 0.1)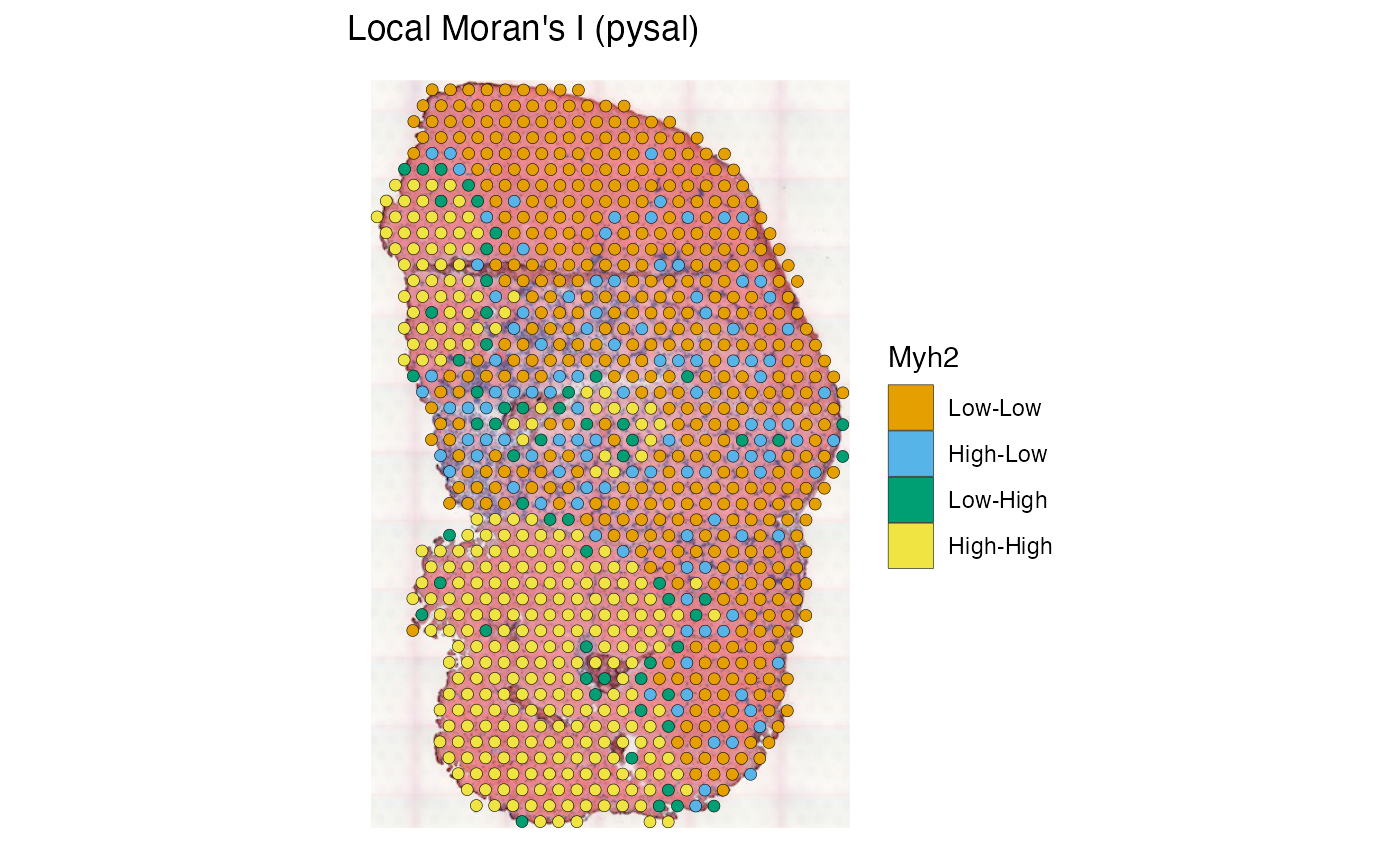

We see that regions with higher Myh2 expression also have stronger spatial autocorrelation. It is interesting to see how spatial autocorrelation relates to gene expression level, much as finding how variance relates to mean in the expression of each gene, which usually indicates overdispersion compared to Poisson in scRNA-seq and Visium data:

df <- data.frame(myh2 = logcounts(sfe_tissue)[rowData(sfe_tissue)$symbol == "Myh2",],
                 Ii = localResult(sfe_tissue, "localmoran", "Myh2", 
                                  swap_rownames = "symbol")[,"Ii"])
ggplot(df, aes(myh2, Ii)) + geom_point(alpha = 0.3) +
    labs(x = "Myh2 (log counts)", y = "localmoran")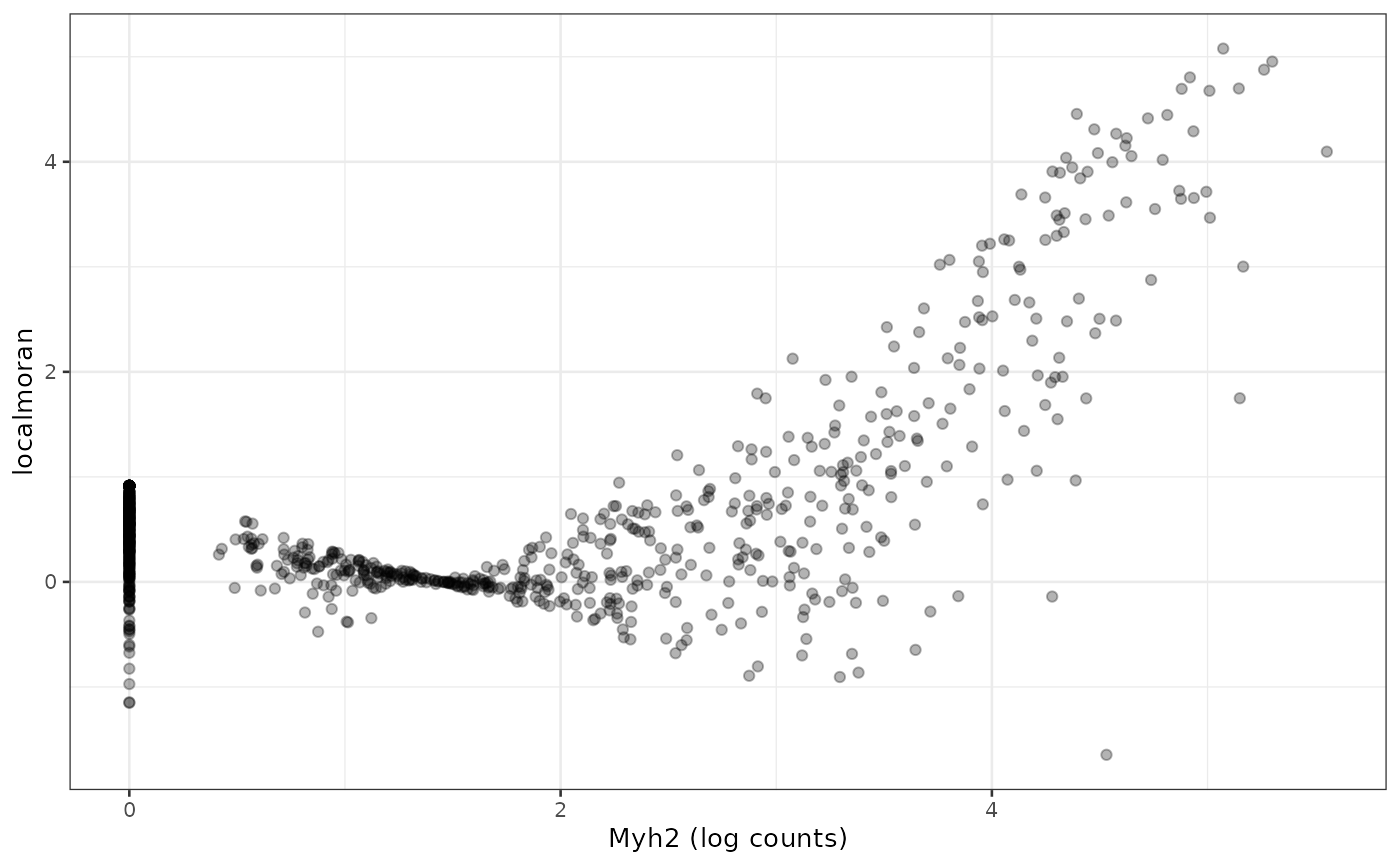

For this gene, Visium spots with higher expression also tend to have higher local Moran’s I, but this may or may not apply to other genes.

Local spatial analyses often return a matrix or data frame. The plotLocalResult() function has a default column for each local spatial method, but other columns can be plotted as well. Use the localResultAttrs() function to see which columns are present, and use the attribute argument to specify which column to plot.

localResultAttrs(sfe_tissue, "localmoran", "Myh2", swap_rownames = "symbol")
#>  [1] "Ii"             "E.Ii"           "Var.Ii"         "Z.Ii"          
#>  [5] "Pr(z != E(Ii))" "mean"           "median"         "pysal"         
#>  [9] "-log10p"        "-log10p_adj"

Some local spatial methods return p-values at each location, in a column with name like Pr(z != E(Ii)), where the test is two sided (default, can be changed with the alternative argument in runUnivariate() which is passed to the relevant underlying function in spdep). Negative log of the p-value is computed to facilitate visualization, and the p-value is corrected for multiple hypothesis testing with p.adjustSP() in spdep, where the number of tests is the number of neighbors of each location rather than the total number of locations (-log10p_adj).

plotLocalResult(sfe_tissue, "localmoran", features = "Myh2", 
                colGeometryName = "spotPoly", attribute = "-log10p_adj", divergent = TRUE,
                diverge_center = -log10(0.05), swap_rownames = "symbol",
                image_id = "lowres", color = "black",
                linewidth = 0.1)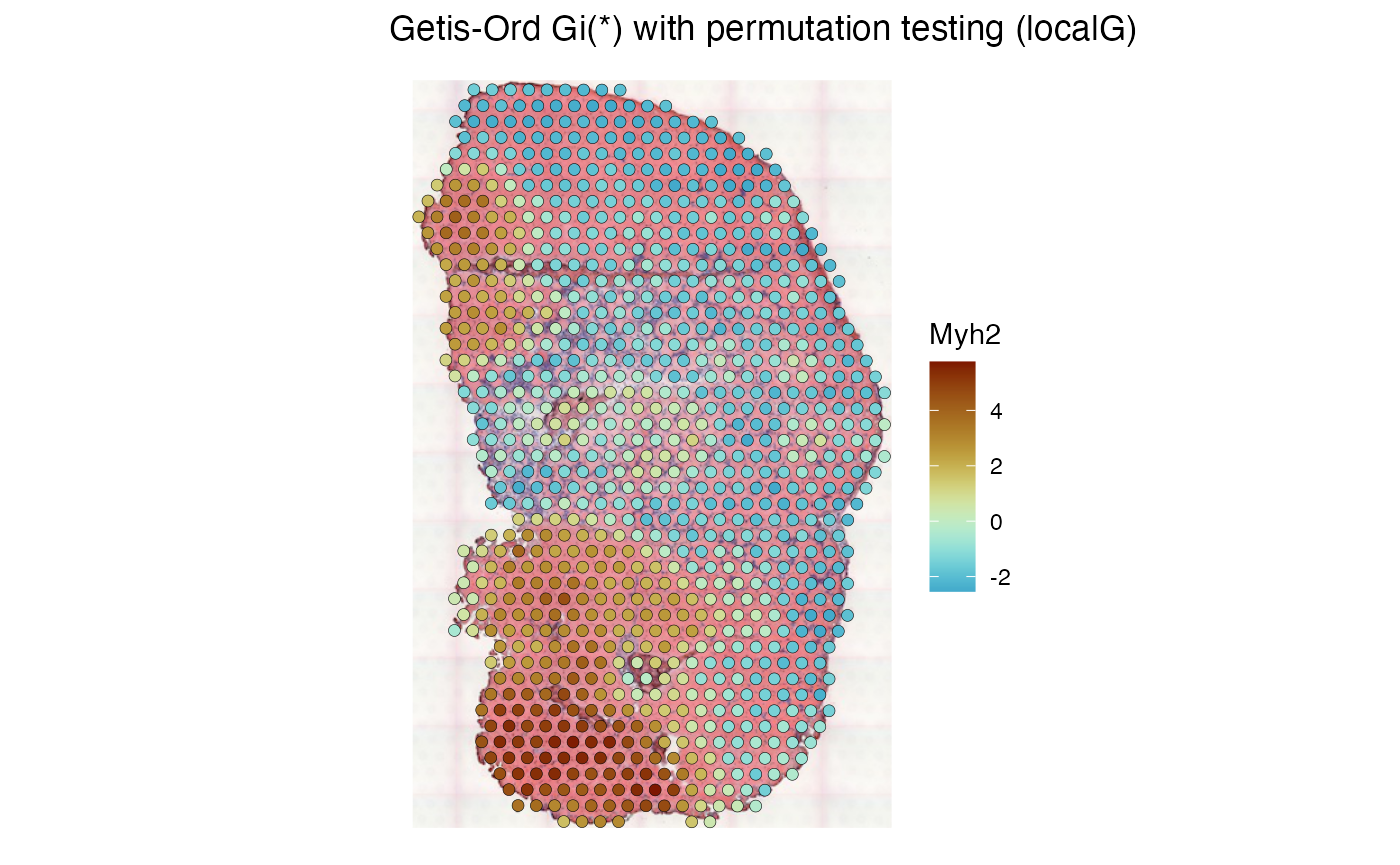

In this plot and all following plots of p-values, a divergent palette is used to show locations that are significant after adjusting for multiple testing and those that are not significant in different colors. The center of the divergent palette is p = 0.05, so the brown spots are significant while a dark blue means really not significant.

The “pysal” column displays the quadrants relative to the means in the Moran plot. The result is similar to that from k-means clustering shown above.

plotLocalResult(sfe_tissue, "localmoran", features = "Myh2", 
                colGeometryName = "spotPoly", attribute = "pysal", 
                swap_rownames = "symbol", image_id = "lowres", color = "black",
                linewidth = 0.1)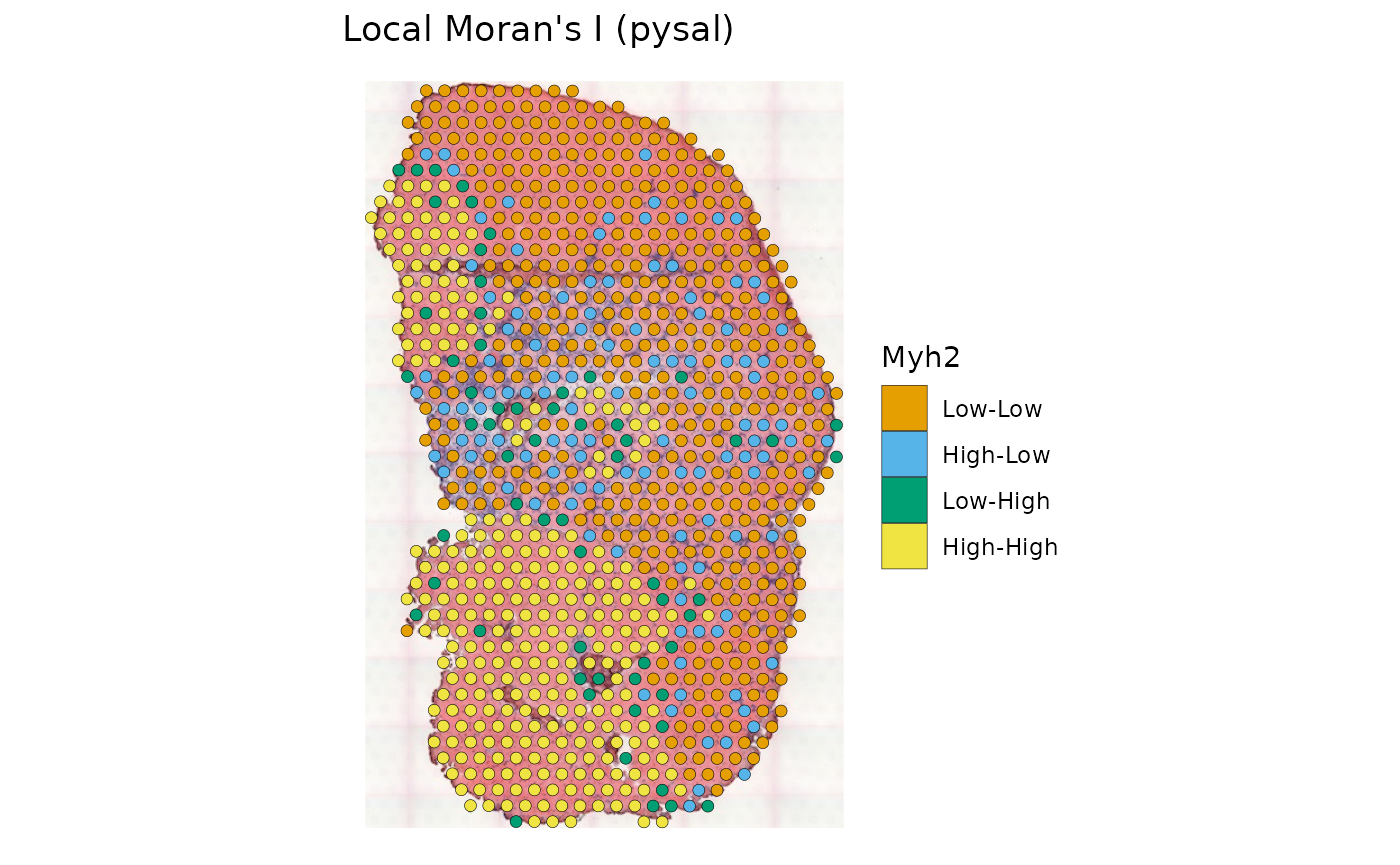

Getis-Ord Gi*

Getis-Ord Gi* is used to find hotspots and coldspots of a feature in space. A hotspot is a cluster of high values in space, and a coldspot is a cluster of low values in space. Getis-Ord Gi* is essentially the z-score of the spatially lagged value of the feature at each location $i$ ($\sum_j w_{ij} x_j$), where $w_{ij}$ is the spatial weight. In the original publication for Getis-Ord Gi* from 1992 (Getis and Ord 1992), the spatial weight is a distance-based binary weight indicating whether another location is within a certain distance from each location $i$. Getis-Ord Gi excludes the location $i$ itself in the computation of mean and variance of the lagged value, while Gi* includes the location $i$ itself. Usually Gi and Gi* yield similar results. The mean and variance used in the z-score differ in Gi and Gi* and is described in this paper from 1995 (J. K. Ord and Getis 1995) and derived in (Getis and Ord 1992).

Binary weights are recommended for Getis-Ord Gi*.

colGraph(sfe_tissue, "visium_B") <- findVisiumGraph(sfe_tissue, style = "B")

sfe_tissue <- runUnivariate(sfe_tissue, type = "localG_perm", features = "Myh2",
                            colGraphName = "visium_B", include_self = TRUE,
                            swap_rownames = "symbol")

plotLocalResult(sfe_tissue, "localG_perm", features = "Myh2", 
                colGeometryName = "spotPoly", divergent = TRUE,
                diverge_center = 0, image_id = "lowres", swap_rownames = "symbol", 
                color = "black", linewidth = 0.1)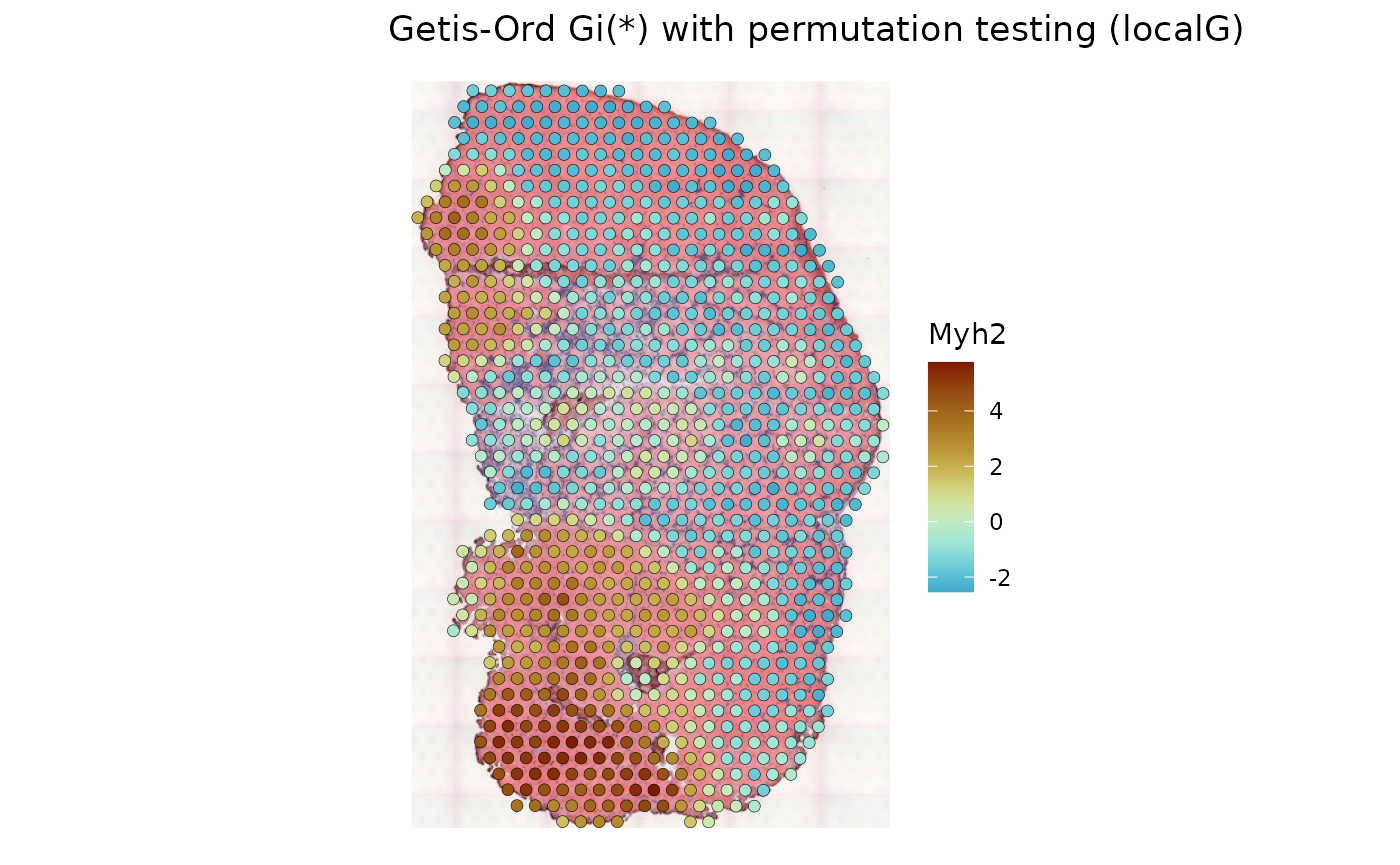

High values of Gi* indicate hotspots, while low values of Gi* indicate coldspots.

localResultAttrs(sfe_tissue, "localG_perm", "Myh2", swap_rownames = "symbol")
#>  [1] "localG"             "Gi"                 "E.Gi"              
#>  [4] "Var.Gi"             "StdDev.Gi"          "Pr(z != E(Gi))"    
#>  [7] "Pr(z != E(Gi)) Sim" "Pr(folded) Sim"     "Skewness"          
#> [10] "Kurtosis"           "-log10p Sim"        "-log10p_adj Sim"   
#> [13] "cluster"

Plot the pseudo-p-values from the simulation

plotLocalResult(sfe_tissue, "localG_perm", features = "Myh2", 
                attribute = "-log10p_adj Sim",
                colGeometryName = "spotPoly", divergent = TRUE,
                diverge_center = -log10(0.05), swap_rownames = "symbol",
                image_id = "lowres")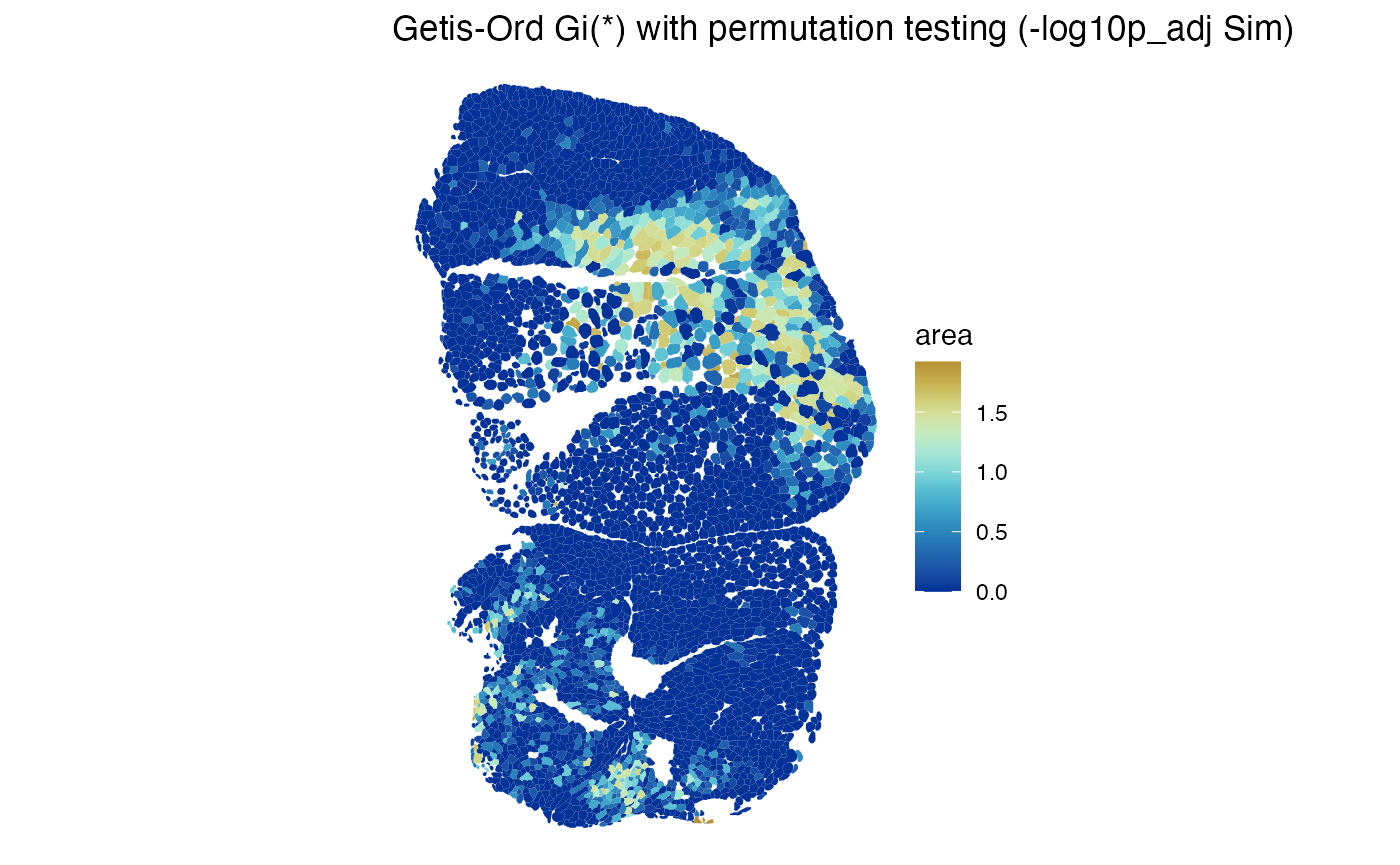

The hotspots are as expected. Here warm color indicates adjusted $p < 0.05$.

Local results can also be computed for annotation geometries.

annotGraph(sfe_tissue, "myofiber_poly2nb_B") <- 
  findSpatialNeighbors(sfe_tissue, type = "myofiber_simplified", MARGIN = 3,
                       method = "poly2nb", zero.policy = TRUE, style = "B")
#> Warning in (function (pl, row.names = NULL, snap = NULL, queen = TRUE, useC = TRUE, : some observations have no neighbours;
#> if this seems unexpected, try increasing the snap argument.
#> Warning in (function (pl, row.names = NULL, snap = NULL, queen = TRUE, useC = TRUE, : neighbour object has 75 sub-graphs;
#> if this sub-graph count seems unexpected, try increasing the snap argument.

sfe_tissue <- annotGeometryUnivariate(sfe_tissue, "localG_perm", "area", 
                                      annotGeometryName = "myofiber_simplified",
                                      annotGraphName = "myofiber_poly2nb_B",
                                      include_self = TRUE, zero.policy = TRUE)

plotLocalResult(sfe_tissue, "localG_perm", "area", 
                annotGeometryName = "myofiber_simplified",
                divergent = TRUE, diverge_center = 0)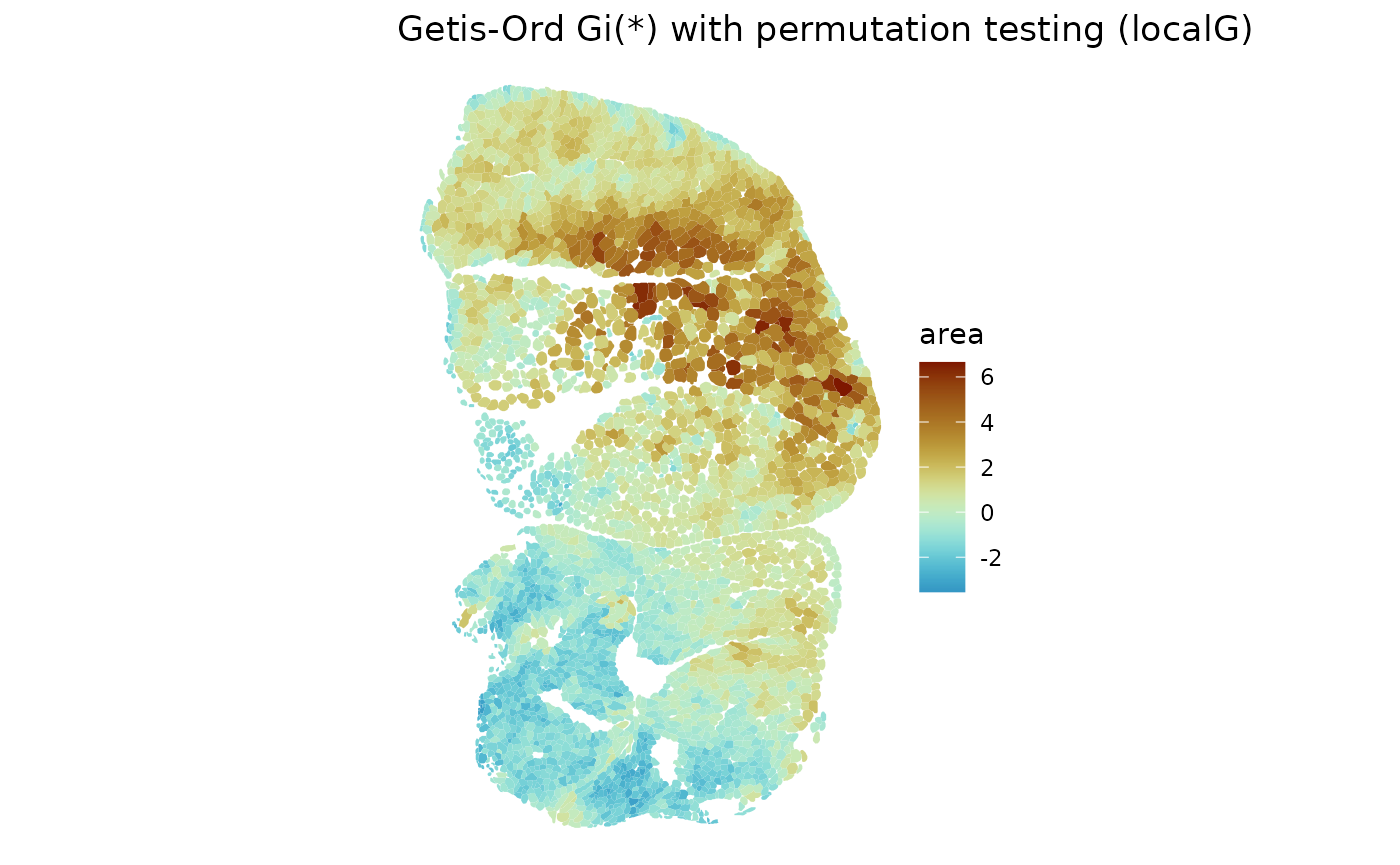

plotLocalResult(sfe_tissue, "localG_perm", "area", 
                annotGeometryName = "myofiber_simplified",
                attribute = "-log10p_adj Sim",
                divergent = TRUE, diverge_center = -log10(0.05))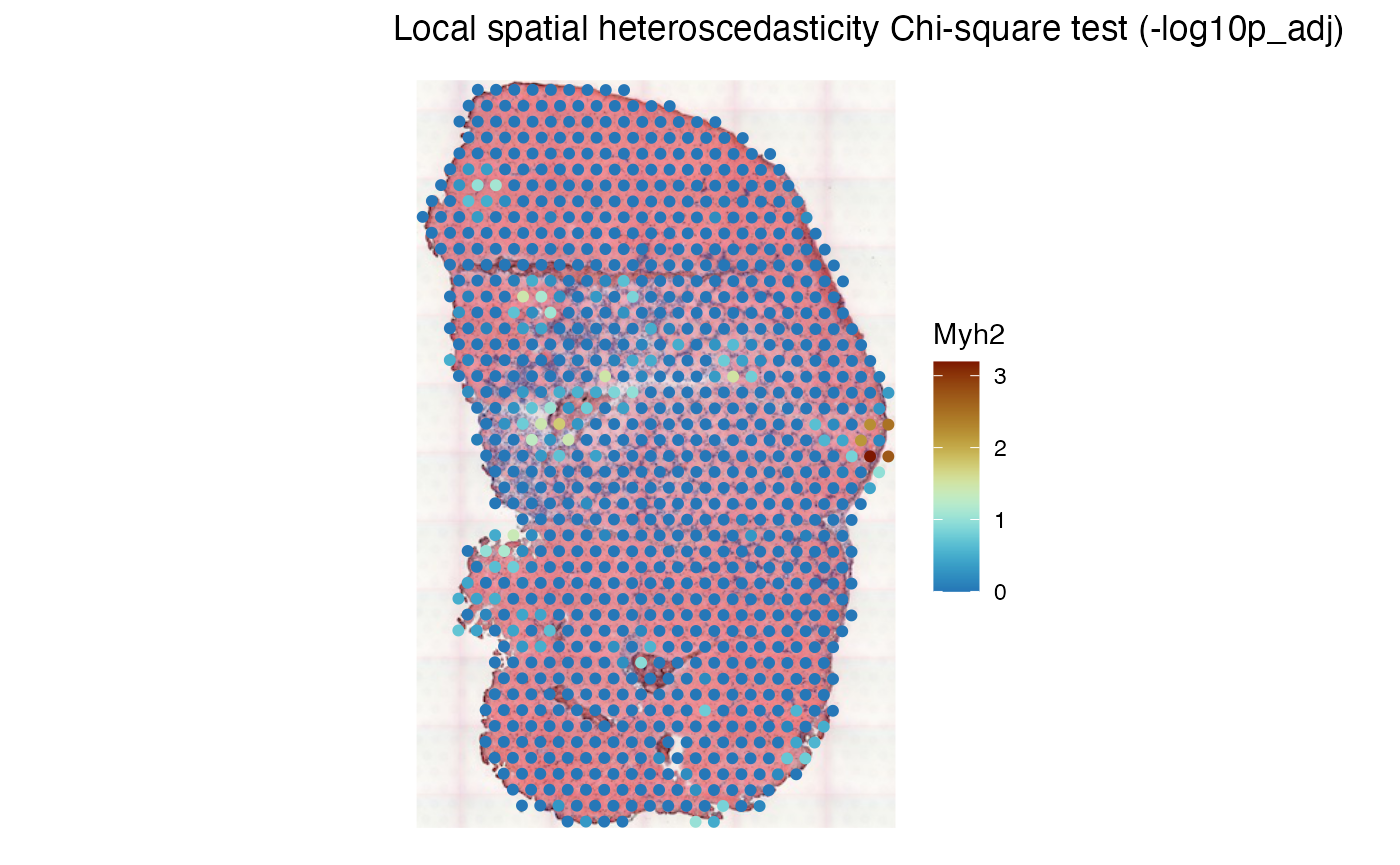

The hotspots and coldspots are as expected. Warm color indicates adjusted $p < 0.05$.

Local spatial heteroscedasticity (LOSH)

LOSH (J. Keith Ord and Getis 2012) is defined as

$$H_i = \frac{\sum_j w_{ij}\left| e_j \right|^a}{h_1\sum_j w_{ij}}$$

where$h_1 = \sum_i \left| e_i \right|^a/n$, $e_j = x_j - \bar{x}_j$, and

$$\bar{x}_j = \frac{\sum_j w_{jk}x_k}{\sum_j w_{jk}}.$$

By default, $a = 2$ so LOSH is like a local variance. See (J. Keith Ord and Getis 2012) for more details and interpretation.

sfe_tissue <- runUnivariate(sfe_tissue, "LOSH.cs", "Myh2", 
                            colGraphName = "visium", swap_rownames = "symbol")

plotLocalResult(sfe_tissue, "LOSH.cs", features = "Myh2", 
                colGeometryName = "spotPoly", swap_rownames = "symbol",
                image_id = "lowres")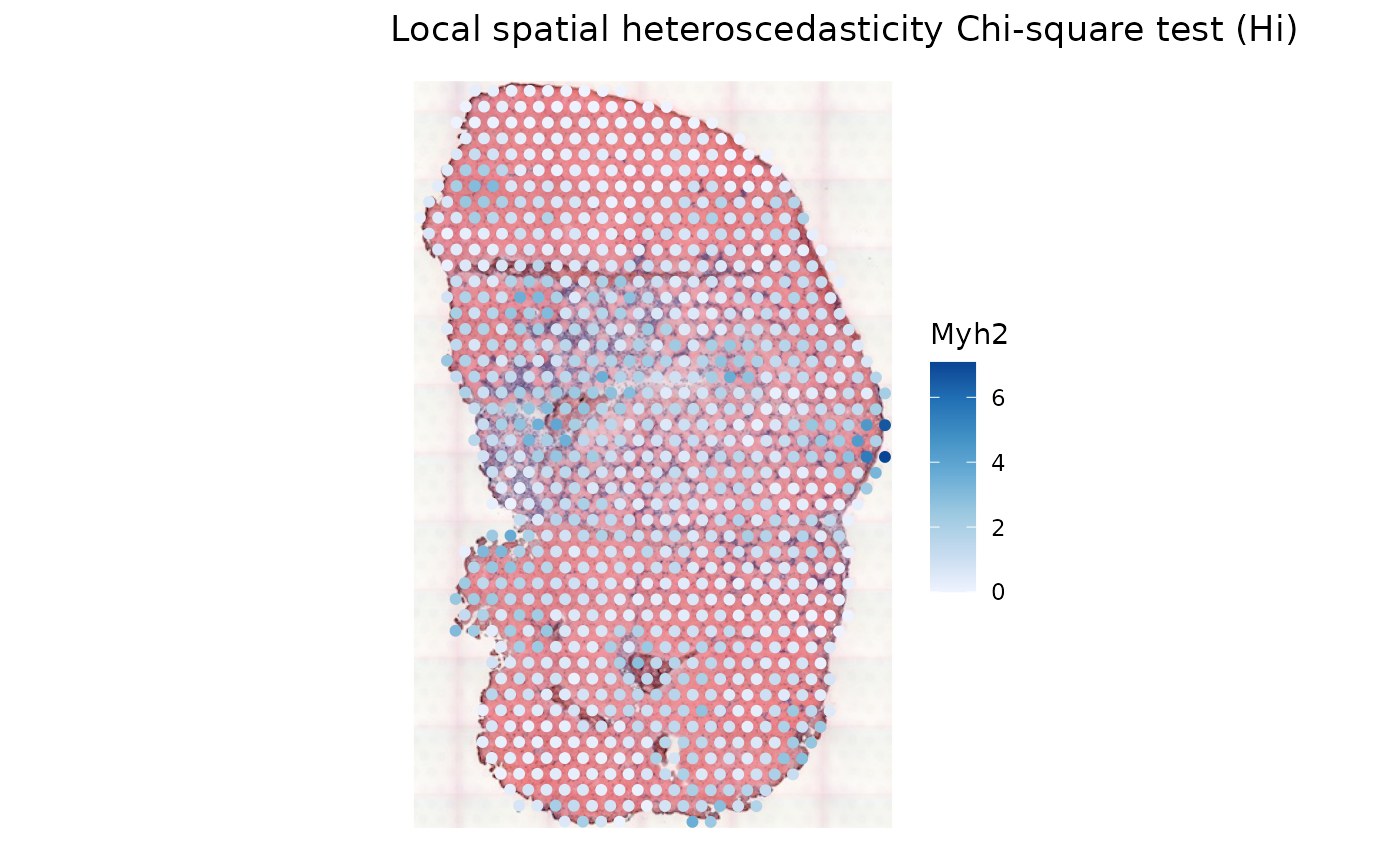

For this gene, it isn’t clear whether LOSH relates to gene expression levels.

localResultAttrs(sfe_tissue, "LOSH.cs", "Myh2", swap_rownames = "symbol")
#> [1] "Hi"          "E.Hi"        "Var.Hi"      "Z.Hi"        "x_bar_i"    
#> [6] "ei"          "Pr()"        "-log10p"     "-log10p_adj"

While Voyager does wrap LOSH.mc() to perform permutation testing of LOSH, this is very time consuming. A chi-squared approximation is described in the 2012 LOSH paper to account for non-normality of the data and to approximate the mean and variance of the permutation distributions, so p-values of LOSH can be more quickly computed, with LOSH.cs().

plotLocalResult(sfe_tissue, "LOSH.cs", features = "Myh2", 
                attribute = "-log10p_adj", colGeometryName = "spotPoly",
                divergent = TRUE, diverge_center = -log10(0.05),
                swap_rownames = "symbol", image_id = "lowres") +
    theme_void()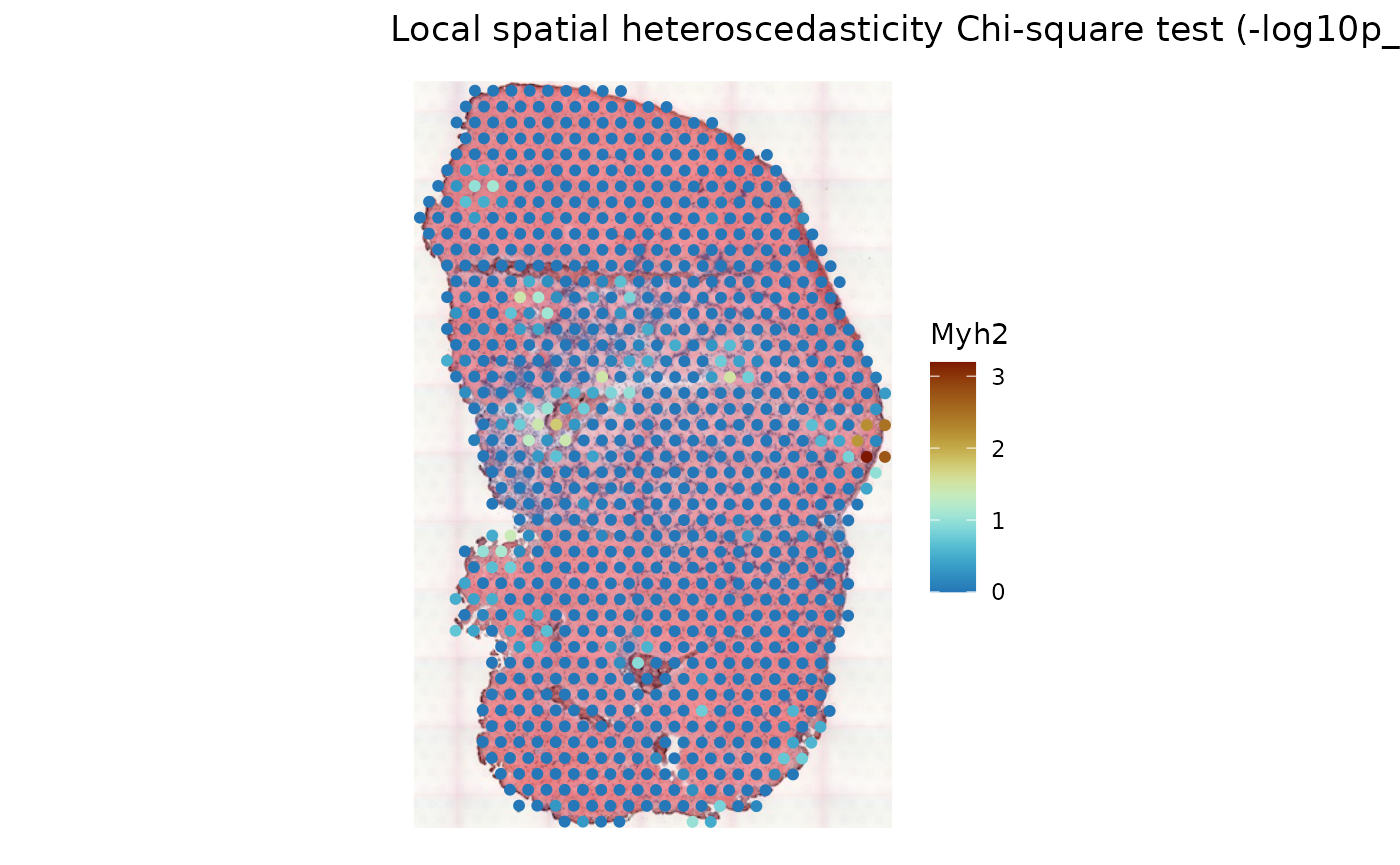

For this gene, the local conditions are mostly homogenous, except for a few spots most at the injury site. Warm color indicates adjusted $p < 0.05$.

Caveats

1. The H&E image can alter perception of the colors of the geometries.
2. Only 2D data is supported at present, although in principle, sf and GEOS support 3D data.
3. Spatial neighborhoods only make sense within the same tissue section. Then what to do with multiple tissue sections, from biological replica, and from different conditions? For the mouse brain, different biological replica can be registered to the Allen Common Coordinate Framework (CCF) to be spatially comparable. Indeed, it would be interesting to see the biological variability of healthy wild type gene expression at the same fine scaled region in the brain. However, there is no CCF for tissues without a stereotypical structure, such as adipose and skeletal muscle. We don’t have a good solution to spatially compare different tissue sections yet. Perhaps global spatial statistics over the whole section or histological regions within the section can be compared. The problem remains to select the most informative metrics to compare. Perhaps a spatially-informed dimension reduction method, taking not only the gene count matrix, but also the adjacency matrices of the spatial neighborhood graphs (different sections will be different blocks in the matrix) projecting the cells or Visium spots from different sections into a shared low dimensional space can facilitate the comparison. Here batch effect must be corrected, and the dimension reduction should be interpretable, and scalable.

Session info

sessionInfo()
#> R version 4.4.2 (2024-10-31)
#> Platform: x86_64-pc-linux-gnu
#> Running under: Ubuntu 22.04.5 LTS
#> 
#> Matrix products: default
#> BLAS:   /usr/lib/x86_64-linux-gnu/openblas-pthread/libblas.so.3 
#> LAPACK: /usr/lib/x86_64-linux-gnu/openblas-pthread/libopenblasp-r0.3.20.so;  LAPACK version 3.10.0
#> 
#> locale:
#>  [1] LC_CTYPE=C.UTF-8       LC_NUMERIC=C           LC_TIME=C.UTF-8       
#>  [4] LC_COLLATE=C.UTF-8     LC_MONETARY=C.UTF-8    LC_MESSAGES=C.UTF-8   
#>  [7] LC_PAPER=C.UTF-8       LC_NAME=C              LC_ADDRESS=C          
#> [10] LC_TELEPHONE=C         LC_MEASUREMENT=C.UTF-8 LC_IDENTIFICATION=C   
#> 
#> time zone: UTC
#> tzcode source: system (glibc)
#> 
#> attached base packages:
#> [1] stats4    stats     graphics  grDevices utils     datasets  methods  
#> [8] base     
#> 
#> other attached packages:
#>  [1] reticulate_1.40.0              dplyr_1.1.4                   
#>  [3] bluster_1.16.0                 BiocParallel_1.40.0           
#>  [5] patchwork_1.3.0                scales_1.3.0                  
#>  [7] sf_1.0-19                      SFEData_1.8.0                 
#>  [9] scran_1.34.0                   scater_1.34.0                 
#> [11] ggplot2_3.5.1                  scuttle_1.16.0                
#> [13] SingleCellExperiment_1.28.1    SummarizedExperiment_1.36.0   
#> [15] Biobase_2.66.0                 GenomicRanges_1.58.0          
#> [17] GenomeInfoDb_1.42.0            IRanges_2.40.0                
#> [19] S4Vectors_0.44.0               BiocGenerics_0.52.0           
#> [21] MatrixGenerics_1.18.0          matrixStats_1.4.1             
#> [23] Voyager_1.8.1                  SpatialFeatureExperiment_1.9.4
#> 
#> loaded via a namespace (and not attached):
#>   [1] splines_4.4.2             filelock_1.0.3           
#>   [3] bitops_1.0-9              tibble_3.2.1             
#>   [5] R.oo_1.27.0               lifecycle_1.0.4          
#>   [7] edgeR_4.4.0               lattice_0.22-6           
#>   [9] MASS_7.3-61               magrittr_2.0.3           
#>  [11] limma_3.62.1              sass_0.4.9               
#>  [13] rmarkdown_2.29            jquerylib_0.1.4          
#>  [15] yaml_2.3.10               metapod_1.14.0           
#>  [17] sp_2.1-4                  cowplot_1.1.3            
#>  [19] RColorBrewer_1.1-3        DBI_1.2.3                
#>  [21] multcomp_1.4-26           abind_1.4-8              
#>  [23] spatialreg_1.3-5          zlibbioc_1.52.0          
#>  [25] purrr_1.0.2               R.utils_2.12.3           
#>  [27] RCurl_1.98-1.16           TH.data_1.1-2            
#>  [29] rappdirs_0.3.3            sandwich_3.1-1           
#>  [31] GenomeInfoDbData_1.2.13   ggrepel_0.9.6            
#>  [33] irlba_2.3.5.1             terra_1.7-83             
#>  [35] units_0.8-5               RSpectra_0.16-2          
#>  [37] dqrng_0.4.1               pkgdown_2.1.1            
#>  [39] DelayedMatrixStats_1.28.0 codetools_0.2-20         
#>  [41] DropletUtils_1.26.0       DelayedArray_0.32.0      
#>  [43] tidyselect_1.2.1          UCSC.utils_1.2.0         
#>  [45] memuse_4.2-3              farver_2.1.2             
#>  [47] ScaledMatrix_1.14.0       viridis_0.6.5            
#>  [49] BiocFileCache_2.14.0      jsonlite_1.8.9           
#>  [51] BiocNeighbors_2.0.0       e1071_1.7-16             
#>  [53] survival_3.7-0            systemfonts_1.1.0        
#>  [55] dbscan_1.2-0              tools_4.4.2              
#>  [57] ggnewscale_0.5.0          ragg_1.3.3               
#>  [59] Rcpp_1.0.13-1             glue_1.8.0               
#>  [61] gridExtra_2.3             SparseArray_1.6.0        
#>  [63] mgcv_1.9-1                xfun_0.49                
#>  [65] EBImage_4.48.0            HDF5Array_1.34.0         
#>  [67] withr_3.0.2               BiocManager_1.30.25      
#>  [69] fastmap_1.2.0             boot_1.3-31              
#>  [71] rhdf5filters_1.18.0       fansi_1.0.6              
#>  [73] spData_2.3.3              digest_0.6.37            
#>  [75] rsvd_1.0.5                mime_0.12                
#>  [77] R6_2.5.1                  textshaping_0.4.0        
#>  [79] colorspace_2.1-1          wk_0.9.4                 
#>  [81] LearnBayes_2.15.1         jpeg_0.1-10              
#>  [83] RSQLite_2.3.8             R.methodsS3_1.8.2        
#>  [85] utf8_1.2.4                generics_0.1.3           
#>  [87] data.table_1.16.2         class_7.3-22             
#>  [89] httr_1.4.7                htmlwidgets_1.6.4        
#>  [91] S4Arrays_1.6.0            spdep_1.3-6              
#>  [93] pkgconfig_2.0.3           scico_1.5.0              
#>  [95] gtable_0.3.6              blob_1.2.4               
#>  [97] XVector_0.46.0            htmltools_0.5.8.1        
#>  [99] fftwtools_0.9-11          png_0.1-8                
#> [101] SpatialExperiment_1.16.0  knitr_1.49               
#> [103] rjson_0.2.23              curl_6.0.1               
#> [105] coda_0.19-4.1             nlme_3.1-166             
#> [107] proxy_0.4-27              cachem_1.1.0             
#> [109] zoo_1.8-12                rhdf5_2.50.0             
#> [111] BiocVersion_3.20.0        KernSmooth_2.23-24       
#> [113] parallel_4.4.2            vipor_0.4.7              
#> [115] AnnotationDbi_1.68.0      desc_1.4.3               
#> [117] s2_1.1.7                  pillar_1.9.0             
#> [119] grid_4.4.2                vctrs_0.6.5              
#> [121] BiocSingular_1.22.0       dbplyr_2.5.0             
#> [123] beachmat_2.22.0           sfheaders_0.4.4          
#> [125] cluster_2.1.6             beeswarm_0.4.0           
#> [127] evaluate_1.0.1            isoband_0.2.7            
#> [129] zeallot_0.1.0             magick_2.8.5             
#> [131] mvtnorm_1.3-2             cli_3.6.3                
#> [133] locfit_1.5-9.10           compiler_4.4.2           
#> [135] rlang_1.1.4               crayon_1.5.3             
#> [137] labeling_0.4.3            classInt_0.4-10          
#> [139] fs_1.6.5                  ggbeeswarm_0.7.2         
#> [141] viridisLite_0.4.2         deldir_2.0-4             
#> [143] Biostrings_2.74.0         munsell_0.5.1            
#> [145] tiff_0.1-12               Matrix_1.7-1             
#> [147] ExperimentHub_2.14.0      sparseMatrixStats_1.18.0 
#> [149] bit64_4.5.2               Rhdf5lib_1.28.0          
#> [151] KEGGREST_1.46.0           statmod_1.5.0            
#> [153] AnnotationHub_3.14.0      igraph_2.1.1             
#> [155] memoise_2.0.1             bslib_0.8.0              
#> [157] bit_4.5.0

References

Anselin, Luc. 1995. “Local Indicators of Spatial Association—LISA.” Geogr. Anal. 27 (2): 93–115.

Assunção, R M, and E A Reis. 1999. “A New Proposal to Adjust Moran’s I for Population Density.” Stat. Med. 18 (16): 2147–62.

Fotheringham, A Stewart. 2009. “‘The Problem of Spatial Autocorrelation’ and Local Spatial Statistics.” Geogr. Anal. 41 (4): 398–403.

Getis, Arthur, and J Keith Ord. 1992. “The Analysis of Spatial Association by Use of Distance Statistics.” In Perspectives on Spatial Data Analysis, edited by Luc Anselin and Sergio J Rey, 127–45. Berlin, Heidelberg: Springer Berlin Heidelberg.

Griffith, Daniel A. 2010. “The Moran Coefficient for Non-Normal Data.” J. Stat. Plan. Inference 140 (11): 2980–90.

Lun, Aaron T L, Davis J McCarthy, and John C Marioni. 2016. “A Step-by-Step Workflow for Low-Level Analysis of Single-Cell RNA-seq Data with Bioconductor.” F1000Res. 5 (August): 2122.

McKellar, David W, Lauren D Walter, Leo T Song, Madhav Mantri, Michael F Z Wang, Iwijn De Vlaminck, and Benjamin D Cosgrove. 2021. “Large-Scale Integration of Single-Cell Transcriptomic Data Captures Transitional Progenitor States in Mouse Skeletal Muscle Regeneration.” Commun. Biol. 4 (1): 1280.

Ord, J Keith, and Arthur Getis. 2012. “Local Spatial Heteroscedasticity (LOSH).” Ann. Reg. Sci. 48 (2): 529–39.

Ord, J K, and Arthur Getis. 1995. “Local Spatial Autocorrelation Statistics: Distributional Issues and an Application.” Geogr. Anal. 27 (4): 286–306.

Wang, Chao, Feng Yue, and Shihuan Kuang. 2017. “Muscle Histology Characterization Using H&E Staining and Muscle Fiber Type Classification Using Immunofluorescence Staining.” Bio Protoc. 7 (10).